From Wikipedia, the free encyclopedia

It has been suggested that this article or section be merged into Axonometric projection. (Discuss)

Isometric projection is a form of graphical projection, more specifically, a form of axonometric projection. It is a method of visually representing three-dimensional objects in two dimensions, in which the three coordinate axes appear equally foreshortened and the angles between any two of them are 120 degrees.

Isometric projection is one of the projections used in technical and engineering drawings.

Overview

The term "isometric" comes from the Greek for "equal measure", reflecting that the scale along each axis of the projection is the same (this is not true of some other forms of graphical projection).

Isometric drawing of a cube.

An isometric view of an object can be obtained by choosing the viewing direction in a way that the angles between the projection of the x, y, and z axes are all the same, or 120°. For example when taking a cube, this is done by first looking straight towards one face. Next the cube is rotated ±45° about the vertical axis, followed by a rotation of approximately ±35.264° (precisely arcsin(tan 30°) ) about the horizontal axis. Note that with the cube (see image) the perimeter of the 2D drawing is a perfect regular hexagon: all the black lines are of equal length and all the cube's faces are the same area.

In a similar way an isometric view can be obtained for example in a 3D scene editor. Starting with the camera aligned parallel to the floor and aligned to the coordinate axes, it is first rotated downwards around the horizontal axes by about 35.264° as above, and then rotated ±45° around the vertical axes.

Another way in which isometric projection can be visualized is by considering a view within a cubical room starting in an upper corner and looking towards the opposite, lower corner. The x-axis extends diagonally down and right, the y-axis extends diagonally down and left, and the z-axis is straight up. Depth is also shown by height on the image. Lines drawn along the axes are at 120° to one another.

Mathematics

There are 8 different orientations to obtain an isometric view, depending into which octant the viewer looks. The isometric transform from a point a_x,y,z in 3D space to a point b_x,y in 2D space looking into the first octant can be written mathematically with rotation matrices as:

where 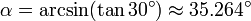and . As explained above, this is a rotation around the vertical (here y) axis by β, followed by a rotation around the horizontal (here x) axis by α. This is then followed by an orthographic projection to the x-y plane:

The other seven possibilities are obtained by either rotating to the opposite sides or not, and then inverting the view direction or not.^[1]

From: http://en.wikipedia.org/wiki/Isometric_perspective

Isometric Projection

An isometric projection is defined by the property, that all the axes have the same metric (isometric, Greek: "equal measure"). Let's draw a cube to visualize what this means.

All the cube's edges have the same length. Furthermore, because the angles between sides all are 120°, all sides are symmetric rhombuses, meaning that the surface of each side is equal. Also note, that the perimeter of the shown cube is a perfect hexagon.

It is easy to see, that the angles at the other side of the edges measure 180°-120°=60°. Because such an angle plus a make a right angle, a=90°-60°=30°.

But the angle a also is defined by a=arctan(h/w)=30° (or, more accurately, to reflect the involved triangle, by a=arctan((h/2)/(w/2))=30°; but this does not make any difference). For the relationship between h and w therefore must be true, that h/w=sin(30°)/cos(30°)=tan(30°)=0.57735, or probably more convenient, h/w=1/sqrt(3).