http://en.wikipedia.org/wiki/Sorting_algorithm#Comparison_of_algorithms
In computer science, a sorting algorithm is an algorithm that
puts elements of a list in a certain order.
The most-used orders are numerical order andlexicographical order. Efficient sorting is
important for optimizing the use of other algorithms (such as search and merge algorithms)
that require sorted lists to work correctly; it is also often useful for canonicalizing data and
for producing human-readable output. More formally, the output must satisfy two conditions:
- The output is in nondecreasing order (each element is no smaller than the previous element according to the desired total
order); - The output is a permutation, or reordering, of the input.
Since the dawn of computing, the sorting problem has attracted a great deal of research, perhaps due to the complexity of solving it efficiently despite its simple, familiar statement. For example, bubble
sort was analyzed as early as 1956.[1] Although
many consider it a solved problem, useful new sorting algorithms are still being invented (for example, library
sort was first published in 2004). Sorting algorithms are prevalent in introductory computer science classes, where the abundance of algorithms for the problem provides a gentle introduction to a variety of core algorithm concepts, such as big
O notation, divide and conquer algorithms, data
structures, randomized algorithms, best,
worst and average case analysis, time-space tradeoffs, and lower
bounds.
Contents[hide] |
[edit]Classification
Sorting algorithms used in computer science are often classified by:
- Computational complexity (worst, average and best behaviour)
of element comparisons in terms of the size of the list (n). For typical sorting algorithms good behavior is O(n log n) and bad behavior is O(n2). (See Big
O notation.) Ideal behavior for a sort is O(n), but this is not possible in the average case.Comparison-based
sorting algorithms, which evaluate the elements of the list via an abstract key comparison operation, need at least O(n log n) comparisons for most inputs. - Computational complexity of swaps
(for "in place" algorithms). - Memory usage (and use of other computer resources). In particular, some sorting algorithms are "in
place". Strictly, an in place sort needs only O(1) memory beyond the items being sorted; sometimes O(log(n)) additional memory is considered "in place". - Recursion. Some algorithms are either recursive or non-recursive, while others may be both (e.g., merge sort).
- Stability: stable sorting algorithms maintain the relative order of records with
equal keys (i.e., values). - Whether or not they are a comparison sort. A comparison sort examines
the data only by comparing two elements with a comparison operator. - General method: insertion, exchange, selection, merging, etc.. Exchange sorts include bubble sort and quicksort. Selection sorts include shaker sort and heapsort.
- Adaptability: Whether or not the presortedness of the input affects the running time. Algorithms that take this into account are known to be adaptive.
[edit]Stability
Stable sorting algorithms maintain the relative order of records with equal keys. If all keys are different then this distinction is not necessary. But if there are equal keys, then a sorting algorithm is stable if whenever there are two records (let's say
R and S) with the same key, and R appears before S in the original list, then R will always appear before S in the sorted list. When equal elements are indistinguishable, such as with integers, or more generally, any data where the entire element is the key,
stability is not an issue. However, assume that the following pairs of numbers are to be sorted by their first component:
(4, 2) (3, 7) (3, 1) (5, 6)
In this case, two different results are possible, one which maintains the relative order of records with equal keys, and one which does not:
(3, 7) (3, 1) (4, 2) (5, 6) (order maintained) (3, 1) (3, 7) (4, 2) (5, 6) (order changed)
Unstable sorting algorithms may change the relative order of records with equal keys, but stable sorting algorithms never do so. Unstable sorting algorithms can be specially implemented to be stable. One way of doing this is to artificially extend the key comparison,
so that comparisons between two objects with otherwise equal keys are decided using the order of the entries in the original data order as a tie-breaker. Remembering this order, however, often involves an additionalcomputational
cost.
Sorting based on a primary, secondary, tertiary, etc. sort key can be done by any sorting method, taking all sort keys into account in comparisons (in other words, using a single composite sort key). If a sorting method is stable, it is also possible to sort
multiple times, each time with one sort key. In that case the keys need to be applied in order of increasing priority.
Example: sorting pairs of numbers as above by second, then first component:
(4, 2) (3, 7) (3, 1) (5, 6) (original)
(3, 1) (4, 2) (5, 6) (3, 7) (after sorting by second component) (3, 1) (3, 7) (4, 2) (5, 6) (after sorting by first component)
On the other hand:
(3, 7) (3, 1) (4, 2) (5, 6) (after sorting by first component)
(3, 1) (4, 2) (5, 6) (3, 7) (after sorting by second component,
order by first component is disrupted).
[edit]Comparison
of algorithms
In this table, n is the number of records to be sorted. The columns "Average" and "Worst" give the time complexity in each case, under the assumption that the length of each key is constant, and that therefore all comparisons, swaps, and other needed
operations can proceed in constant time. "Memory" denotes the amount of auxiliary storage needed beyond that used by the list itself, under the same assumption. These are all comparison
sorts. The run time and the memory of algorithms could be measured using various notations like theta, omega, Big-O, small-o, etc. The memory and the run times below are applicable for all the 5 notations.
| Name | Best | Average | Worst | Memory | Stable | Method | Other notes |
|---|---|---|---|---|---|---|---|
| Quicksort |
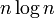 |
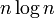 |
 |
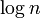 |
Depends | Partitioning |
Quicksort is usually done in place with O(log(n)) stack space.[citation needed] Most implementations are unstable, as stable in-place partitioning is more complex. Naïve variants use an O(n) space array to store the partition.[citation needed] |
| Merge sort |
 |
 |
 |
Depends; worst case is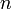 |
Yes | Merging | Used to sort this table in Firefox [2]. |
|
In-place Merge sort |
 |
 |
 |
 |
Yes | Merging |
Implemented in Standard Template Library (STL):[3]; can be implemented as a stable sort based on stable in-place merging: [4] |
| Heapsort |
 |
 |
 |
 |
No | Selection | |
| Insertion sort |
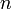 |
 |
 |
 |
Yes | Insertion | O(n + d), where d is the number of inversions |
| Introsort |
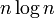 |
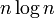 |
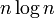 |
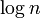 |
No | Partitioning & Selection | Used in SGI STL implementations |
| Selection sort |
 |
 |
 |
 |
|