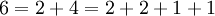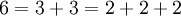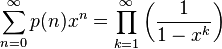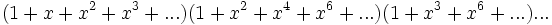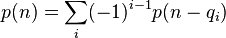21:41:51
分类: C/C++
整数分拆[编辑]
一个正整数可以写成一些正整数的和。在数论上,跟这些和式有关的问题称为整数分拆、整数剖分、整数分割、分割数或切割数。其中最常见的问题就是给定正整数 ,求不同数组
,求不同数组 的数目,符合下面的条件:
的数目,符合下面的条件:
 (
( 的大小不定)
的大小不定)
- 其他附加条件(例如限定“k是偶数”,或“
 不是1就是2”等)
不是1就是2”等)
分割函数p(n)是求符合以上第一、二个条件的数组数目。
例[编辑]
4可以用5种方法写成和式:4, 3+1, 2+2, 2+1+1, 1+1+1+1。因此  。
。
习惯定义  ,若n是负数则置
,若n是负数则置 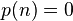 。
。
分割函数p(n)的第几项(包括p(0))为
- 1、1、2、3、5、7、11、15、22、30、42、56、77……(OEIS:A000041)
Ferrers图示与恒等式[编辑]
每种分割方法都可用Ferrers图示表示。
Ferrers图示是将第1行放 个方格,第2行放
个方格,第2行放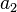 个方格……第
个方格……第 行放
行放 个方格,来表示整数分割的其中一个方法。
个方格,来表示整数分割的其中一个方法。
借助Ferrers图示,可以推导出许多恒等式:
- 给定正整数k和n,n表达成不多于k个正整数之和的方法数目,等于将n分割成任意个不大于k的正整数之和的方法数目。
证明:将表示前者其中一个数组的Ferrers图示沿对角线反射,便得到后者的一个数组。即两者一一对应,因此其数目相同。
例如 k=3,n=6:
| ↔ | ||||
| 6 | = | 1+1+4 | = | 1+1+1+3 |
| ↔ | ||||
| 6 | = | 1+2+3 | = | 1+2+3 |
| ↔ | ||||
| 6 | = | 2+2+2 | = | 3+3 |
此外,
- 上述恒等式的值亦等于将
 表达成刚好
表达成刚好 个正整数之和的方法的数目。
个正整数之和的方法的数目。
- 给定正整数
 。将
。将 表达成两两相异正整数之和的方法的数目,等于将
表达成两两相异正整数之和的方法的数目,等于将 表达成奇数之和的方法的数目。
表达成奇数之和的方法的数目。
例如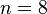 :
:
- 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1
- 7 + 1
- 3 + 3 + 1 + 1
- 5 + 3
- 5 + 1 + 1 + 1
- 3 + 1 + 1 + 1 + 1 + 1
- 8
- 7 + 1
- 6 + 2
- 5 + 3
- 5 + 2 + 1
- 4 + 3 + 1
- 将
 表达成
表达成 个1和
个1和 个2之和,这些方法的数目是第
个2之和,这些方法的数目是第 个斐波那契数。
个斐波那契数。
- 将
 表达成多于1的正整数之和的方法数目是p(n)
表达成多于1的正整数之和的方法数目是p(n)
- p(n-1)。
生成函数[编辑]
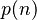 的生成函数是
的生成函数是
当|x|<1,右边可写成:
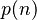 生成函数的倒数为欧拉函数,利用五边形数定理可得到以下的展开式:
生成函数的倒数为欧拉函数,利用五边形数定理可得到以下的展开式:
将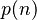 生成函数配合五边形数定理,可以得到以下的递归关系式
生成函数配合五边形数定理,可以得到以下的递归关系式
其中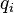 是第
是第 个广义五边形数。
个广义五边形数。
Rademacher级数[编辑]
渐近式:
这式子是1918年哈代和拉马努金,以及1920年J.
V. Uspensky独立发现的。
1937年,Hans
Rademacher得出一个更佳的结果:
其中
-
 。
。
 表示
表示 互质时才计算那项。
互质时才计算那项。 表示戴德金和。这条公式的证明用上了福特圆、法里数列、模群和戴德金η函数 。
表示戴德金和。这条公式的证明用上了福特圆、法里数列、模群和戴德金η函数 。
Elder定理[编辑]
在将 表示成正整数之和的所有和式之中,任意正整数
表示成正整数之和的所有和式之中,任意正整数 作为和项出现在这些式子内的次数,跟每条和式中出现
作为和项出现在这些式子内的次数,跟每条和式中出现 次或以上的正整数数目,相同。
次或以上的正整数数目,相同。
当 时,此定理又称为Stanley定理。
时,此定理又称为Stanley定理。
以 为例:
为例:
- 5
- 4+1
- 3+2
- 3+1+1
- 2+2+1
- 2+1+1+1
- 1+1+1+1+1
- 1的总出现次数:0+1+0+2+1+3+5=12;在每条和式出现1次或以上的数的数目:1+2+2+2+2+2+1=12
- 2的总出现次数:0+0+1+0+2+1+0=4;在每条和式出现2次或以上的数的数目:0+0+0+1+1+1+1=4。
 [编辑]
[编辑]
当限定将 表示成刚好
表示成刚好 个正整数之和时,可以表示为
个正整数之和时,可以表示为 。显然,
。显然, 。
。
- 对于
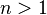 ,
,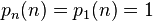
 (OEIS:A004526)
(OEIS:A004526)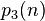 =
=
最接近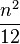 的正整数。(OEIS:A069905)
的正整数。(OEIS:A069905)
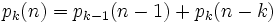
其他常见的问题[编辑]
不少数学家亦有研究按以下方式分拆的方法数目:
- 将正整数写成模p同余r的正整数之和
- 将模p同余r正整数写成的正整数之和[1]
外部链接[编辑]
- Lectures on
Integer Partitions by Herbert S. Wilf
整数划分问题是算法中的一个经典命题之一,有关这个问题的讲述在讲解到递归时基本都涉及到。
所谓整数划分,是指把一个正整数n写成如下形式:
n=m1+m2+m3+....+mi;(其中mi为正整数,并且1<=mi<=n),则{m1,m2,m3,....,mi}为n的一个划分。
如果{m1,m2,m3,....,mi}中的最大值不超过m,即max{m1,m2,m3,....,mi}
<= m,则称它属于n的一个m划分。这里我们记n的m划分的个数为f(n,m);
例如当n=4时,它有5个划分:{4}、{3,1}、{2,2}、{2,1,1}、{1,1,1,1};
注意:4=1+3和4=3+1被认为是同一个划分。
该问题是求出n的所有划分个数,即f(n,n)。下面我们考虑求f(n,m)的方法。
(一)方法一——递归法
根据n和m的关系,考虑下面几种情况:
(1)当n=1时,不论m的值为多少(m>0),只有一种划分,即{1};
(2)当m=1时,不论n的值为多少(n>0),只有一种划分,即{1,1,....1,1,1};
(3)当n=m时,根据划分中是否包含n,可以分为两种情况:
(a)划分中包含n的情况,只有一个,即{n};
(b)划分中不包含n的情况,这时划分中最大的数字也一定比n小,即n的所有(n-1)划分;
因此,f(n,n) = 1 + f(n, n - 1)。
(4)当n<m时,由于划分中不可能出现负数,因此就相当于f(n,n);
(5)当n>m时,根据划分中是否包含m,可以分为两种情况:
(a)划分中包含m的情况,即{m,{x1,x2,x3,...,xi}},其中{x1,x2,x3,...,xi}的和为n-m,可能再次出现m,因此是(n-m)的m划分,因此这种划分个数为f(n-m, m);
(b)划分中不包含m的情况,则划分中所有值都比m小,即n的(m-1)划分,个数为f(n, m - 1);
因此,f(n,m) = f(n - m,m) + f(n, m - 1)。
综合以上各种情况,可以看出,上面的结论具有递归定义的特征,其中(1)和(2)属于回归条件,(3)和(4)属于特殊情况,而情况(5)为通用情况,属于递归的方法,其本质主要是通过减少n或m以达到回归条件,从而解决问题。
其递归表达式如下所示。

(二)方法二——母函数
下面我们从另一个角度,即“母函数”的角度来考虑这个问题。
所谓母函数,即为关于x的一个多项式G(x):
有G(x) = a0 + a1*x + a2*x^2 + a3*x^3 + ......
则我们称G(x)为序列(a0, a1, a2,.....)的母函数。关于母函数的思路我们不做更过分析。
我们从整数划分考虑,假设n的某个划分中,1的出现个数记为a1,2的个数记为a2,.....,i的个数记为ai,
显然有:ak <= n/k(0<= k <=n)
因此n的划分数f(n,n),也就是从1到n这n个数字抽取这样的组合,每个数字理论上可以无限重复出现,即个数随意,使它们的综合为n。显然,数字i可以有如下可能,出现0次(即不出现),1次,2次,......,k次等等。把数字i用(x^i)表示,出现k次的数字i用(x^(i*k))表示,不出现用1表示。
例如,数字2用x^2表示,2个2用x^4表示,3个2用x^6表示,k个2用x^2k表示。
则对于从1到N的所有可能组合结果我们可以表示为:
G(x) = ( 1 + x + x^2 + x^3 + ... + x^n)*(1 + x^2 + x^4 + x^6 + ....)....(1 + x^n)
= g(x,1)*g(x,2)*g(x,3)*....*g(x,n)
= a0 + a1*x + a2*x^2 +...+ an*x^n + ....//展开式
上面的表达式中,每个括号内的多项式代表了数字i的参与到划分中的所有可能情况。因此,该多项式展开后,由于x^a *x^b = x^(a+b),因此x^i就代表了i的划分,展开后(x^i)项的系数也就是i的所有划分个数,即f(n,n)
= an。
由此我们找到了关于整数划分的母函数G(x);剩下的问题就是,我们需要求出G(x)的展开后的所有系数。
为此,我们首先要做多项式乘法,对于我们来说,并不困难。我们把一个关于x的多项式用一个整数数组a[]表示,a[i]代表x^i的系数,即:
g(x) = a[0] + a[1]x + a[2]x^2 + ... + a[n]x^n;
则关于多项式乘法的代码如下,其中数组a和数组b表示两个要相乘的多项式,结果存储到数组c中。
(三)代码实现
-
/*----------------------------------------------
-
* Author :梦醒潇湘love
-
* Date :2013-02-28
-
* Email :9974**140@qq.com
-
* Copyright:anyone
-
-----------------------------------------------*/
-
-
#include <stdio.h>
-
#include <stdlib.h>
-
#include <string.h>
-
-
#define DEBUG
-
//递归法求解整数划分
-
unsigned long GetPartitionCount(int n, int max)
-
{
-
if(n == 1 || max == 1)
-
{
-
return 1;
-
}
-
if(n < max)
-
{
-
return GetPartitionCount(n, n);
-
}
-
if(n == max)
-
{
-
return 1 + GetPartitionCount(n, n - 1);
-
}
-
else
-
{
-
return GetPartitionCount(n - max, max) + GetPartitionCount(n, max - 1);
-
}
-
}
-
-
-
//母函数法求整数划分
-
-
#define MAXNUM 100 //最高次数
-
unsigned long a[MAXNUM];
-
unsigned long b[MAXNUM];
-
unsigned long c[MAXNUM]; //保存结果
-
-
//两个多项式进行乘法,系数分别保存在a和b中,结果保存到c,项的最大次数到MAXNUM
-
void Poly()
-
{
-
int i;
-
int j;
-
memset(c, 0, sizeof(c));
-
for(i = 0; i < MAXNUM; i++)
-
{
-
for(j = 0; j < MAXNUM - i; j++) //j < MAXNUM - i,确保i+j不越界
-
{
-
c[i + j] += a[i] * b[j];
-
}
-
}
-
}
-
//计算前N项的系数,即g(x,1)*g(x,2)*....*g(x,n)的展开结果
-
void Init(int m)
-
{
-
int i;
-
int j;
-
memset(a, 0, sizeof(a));
-
memset(c, 0, sizeof(c));
-
//第一个多项式:g(x) = x^0 + x^1 + x^2 + ... + x^n
-
for(i = 0; i < MAXNUM; i++)
-
{
-
a[i] = 1;
-
}
-
//for(j = 2; j <= MAXNUM; j++)//只能求f(n,n)
-
//通过修改这里,使得可以求f(n,m),对于任意的正整数n,m都适合
-
for(j = 2; j <= m; j++)
-
{
-
memset(b, 0, sizeof(b));
-
//第i个多项式:g(x) = x^0 + x^i + x^(2k) + ...
-
for(i = 0; i <= MAXNUM; i += j)
-
{
-
b[i] = 1;
-
}
-
//多项式相乘:c = a * b
-
Poly();
-
//将结果c保存到a中
-
memcpy(a, c, sizeof(c));
-
}
-
}
-
-
//母函数方法得出整数划分相应的划分数目
-
//n:整数
-
//m:划分方法
-
void CalPrint(int n, int m)
-
{
-
if(n < m)
-
{
-
Init(n);
-
//由于n小于m,此时按n == m打印
-
printf("由于n小于m,所有(%d,%d) = (%d,%d) = %ldn", n, m, n, n, c[n]);
-
}
-
else
-
{
-
-
Init(m);
-
printf("整数划分(%d,%d)方法数目f(%d,%d) = %ldn", n, m, n, m, c[n]);
-
}
-
}
-
-
int main(int argc, char **argv)
-
{
-
int n;
-
int m;
-
unsigned long count;
-
printf("请输入要划分的整数:n");
-
scanf("%d", &n);
-
printf("请输入划分数:n");
-
scanf("%d", &m);
-
if(n <= 0)
-
{
-
fprintf(stderr, "输入的整数不能为非正数.n");
-
return -1;
-
}
-
if(m <= 0)
-
{
-
fprintf(stderr, "输入的划分数不能为非正数.n");
-
return -1;
-
}
-
count = GetPartitionCount(n, m);
-
-
printf("方法一:递归法n");
-
printf("整数划分(%d,%d)的方法数为:%dnn", n, m, count);
-
-
printf("方法二:母函数法n");
-
CalPrint(n,m);
-
-
#ifdef DEBUG
-
int i = 0;
-
for( i = 0; i < MAXNUM; i++)
-
{
-
printf("%9ld ", c[i]);
-
if((i + 1) % 10 == 0)
-
{
-
printf("n");
-
}
-
}
-
printf("n");
-
#endif
-
return 0;
- }
测试结果:

希望母函数的实现是正确的,如果您发现错误,请帮助指出,谢谢您。
参考:http://www.cnblogs.com/hoodlum1980/
下面这个帖子讲的也很好:http://www.cnblogs.com/xiaoxian1369/archive/2011/09/12/2174212.html