学步园

瑞士数学家雅各布·伯努利在考虑“当投掷n粒骰子时，加起来点数总和等于m的可能方式的数目”这个问题时首先使用了母函数方法，

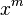并得出可能的数目是的展开式中项的系数。

  查看：http://zh.wikipedia.org/wiki/母函数

由此可以看出:

1.  x的系数是a₁,a₂,…a_{n的单个组合的全体。}

2.  x²的系数是a₁,a₂,…a_n的两个组合的全体。

………

n.  xⁿ的系数是a₁,a₂,….a_n的n个组合的全体（只有1个）。

得到：

母函数又称生成函数。定义是给出序列:a0,a1,a2,.......ak,......,

那么函数G(x)=a0+a1*x+a2*x²+......ak*x^k称为序列a0,a1,a2,.......ak,......的母函数(即生成函数)。

例如：序列1,2,3.......n的生成函数为：G(x)=x+2x²+3x³+........nxⁿ。

特别的当序列为:1，1，1，1，.......1，这个生成函数为:G(x)=x+x²+x³+.......+xⁿ=(1-xⁿ)/(1-x),当-1<x<1时G(x)=1/(1-x)

例 1：使用母函数求出斐波那契数列的通项公式。Fib(n)=Fib(n-1)+Fib(n-2),这里假设Fib(1)=1,Fib(2)=1;

求解这种递推关系的方法是：①、将递推关系变成母函数方程；②、求解母函数方程；③、将母函数变成幂级数形式。

所以斐波那契数列的生成函数为:G(x)=x+x²+2x³+3x⁴+5x⁵+8x⁶..........。

等式两边同时*x有：xG(x)=x²+x³+2x⁴+3x⁵+5x⁶+8x⁷+.......。

相加有：G(x)+xG(x)=x+2x²+3x³+5x⁴+8x⁵+13x⁶+........。

我们对比G(x)可以得到:G(x)+xG(x)=G(x)/x-1;所以我们可以得到:G(x)=x/(1-x-x²)。

可以令:1-x-x²=0,得到两根为:a=(1-√5)/2,b=(1+√5)/2,所以我们可以知道:1-x-x²=(x-x1)(x-x2)=(1-ax)(1-bx);

假设x/(1-x-x²)=m/(1-ax)+n/(1-bx),通分有：x=m(1-bx)+n(1-ax).由系数关系可得m=-1/√5,n=1/√5,所以G(x)=-1/√5(1-bx)+1/√5(1-ax)。

我们可知：1/(1-bx)=1/[1-(1+√5)/2x]是以公比为(1+√5)/2的等比数列，1/(1-ax)是以公比为(1-√5)/2的等比数列，

所以其通项公式为：Fib(n)=1/√5[bⁿ⁺¹-aⁿ⁺¹]。

===================================================================================================================

例题2：若有1克、2克、3克、4克的砝码各一 枚，能称出哪几种重量？各有几种可能方案？

构造母函数，如果用x的指数表示称出的重量，则：
1个1克的砝码可以用函数1+x表示，(前面的这个1表示1克的砝码个数为0)
1个2克的砝码可以用函数1+x²表示，
1个3克的砝码可以用函数1+x³表示，
1个4克的砝码可以用函数1+x⁴表示，

我们拿1+x²来说，前面已经说过，x表示砝码，x的指数表示重量，即这里就是一个质量为2的砝码，

那么前面的1表示什么？1代表重量为2的砝码数量为0个。1其实应该写为：1*x^0,即1代表重量为2的砝码数量为0个。

那么几种砝码的组合情况的用乘积表示有:(1+x)(1+x²)(1+x³)(1+x⁴)=1+x+x²+2x³+2x⁴+2x⁵+2x⁶+2x⁷+x⁸+x⁹+x¹⁰ ,系数即为方案数。

例称出重量为6的物品：①、1，2，3；②、2，4两种方案。

===================================================================================================================

例题4：德.梅其里亚克称重问题

(1)重为a1,a2,a3.....ak的砝码，如何放在天平的两端，记可称重量为n的物体的不同方式为Cn,则Cn的母函数为:

G(x)=(x^-a1+1+x^a1)(x^-a2+1+x^a2).........(x^-ak+1+x^ak) ------ x^-a1表示砝码a1和物体放在同一个托盘内,

x^a1表示砝码和物体放在不同的托盘内,1则为不用这个砝码。

(2)重为a1,a2,a3....ak的砝码，如只可以放在天平的一端，记可称重量为n的物体的不同方式为Cn，则Cn的母函数为：

G(x)=(1+x^a1)(1+x^a2).........(1+x^ak)

==========================================================================================================================

例题5：数的划分，将整数分解为若干个整数(相当于将n个苹果放在n个无区别的盘子里，每个盘子可以放多个，也可以不放)，上一篇博文中有提到。

        假设1出现的次数为记为a1,2出现的次数记为a2.........k出现的次数记为ak,那么生成函数为：

     G(x)=(1+x+x²+x³+x⁴+.....)(1+x²+x⁴+x⁶+x⁸+......)(1+x³+x⁶+x⁹+....)........(1+xⁿ)

     前面的1+x²+x⁴+x⁶+x⁸+......意思是当出现一个2时为x²，当出现两个2时为x⁴.....,为什么当出现n时，只有两项(1+xⁿ)，

因为是将数n划分为若干项，所以不能超过该数，且由数1到n项数依次要<=n/k(k=1.2,3,4...n)。

G（x）=（1+x+x^2+x^3+...）(1+x^2+x^4+...)(1+x^3+x^6+....)....

#include<iostream>  
usingnamespace std;  
  
constint _max = 10001;  
//c1是保存各项质量砝码可以组合的数目  
//c2是中间量，保存没一次的情况  
int c1[_max], c2[_max];    
int main()  
{  
    int nNum;   
    int i,j,k;  
   
    while(cin >> nNum)  
    {  
       for(i=0; i<=nNum; ++i)//首先对c1初始化，由第一个表达式(1+x+x2+..xn)初始化，把质量从0到n的所有砝码都初始化为1 
       {  
           c1[i] = 1;  
           c2[i] = 0;  
       }  
       for(i=2; i<=nNum; ++i)//i从2到n遍历，这里i就是指第i个表达式，母函数关系式里，每一个括号括起来的就是一个表达式
       {  
   
           for(j=0; j<=nNum; ++j)// j从0到n遍历，这里j就是只一个表达式里第j个变量，比如在第二个表达式(1+x2+x4....)里，第j个就是x^2*j.
              for(k=0; k+j<=nNum; k+=i)//k表示的是第j个指数，所以k每次增i（因为第i个表达式的增量是i） 
              {  
                  c2[j+k] += c1[j];  
              }  
           for(j=0; j<=nNum; ++j)//把c2的值赋给c1,而把c2初始化为0，因为c2每次是从一个表达式中开始的  
           {  
              c1[j] = c2[j];  
              c2[j] = 0;  
           }  
       }  
       cout << c1[nNum] << endl;  
    }  
    return 0;  
}  

钱币面值题目： HDU 1085