上回说到,用直线的 N*X - d = 0 的基本公式,可以很方便的判断一个点在直线的前面还是后面,对于三角形、四边形这样的凸多边形,可以按一定的规则把直线组织好,让法线都朝里面,于是对每条边都判断点在哪边,以确定点是在凸多边形的里面还是外面。 以下几个是凸多边形的图,作为回顾:
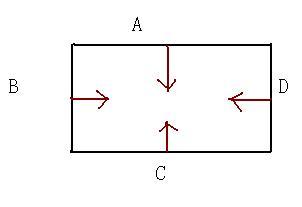
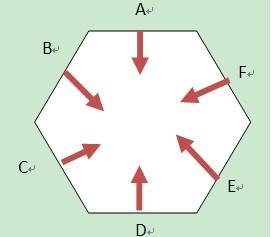
如上面两图。左边是一个四边形,右边是一个六边形。它们都是凸多边形,即任意两个顶点的连接线,都不会穿过其他的边。 为了判断一个点在不在这些凸多边形内,只需要把这个点跟凸多边形的每条边都套用 N*X - d 公式计算它的值 。 公式中的N就是那些直线指向多边形内的箭头所代表的法线,而X就是我们要判断的这个点的(x, y)坐标,d是用来表示直线的一个浮点值。如果这个点跟每条边的 N*X - d 算出的值都大于等于0,
则表示这个点是在凸多边形内。否则有一个小于0就表示它在多边形外。于是对于左边的四边形,可能要套用公式计算1到4次。而右边的六边形则可能需要套用公式计算1到6次。
非常好,对于凸多边形是否包含点的判断,我们都可以通过调用每个边的直线的基本定义来判断。但是对于凹多边形呢, 我们来看下图:
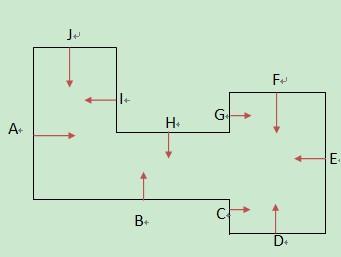
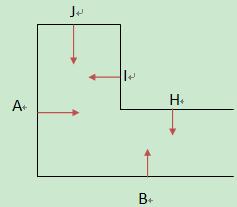
如上图所示,这是一个类似3D室内射击游戏的走廊和房间的一个凹多边形,它由从A到J的10条边组成,每条边也是按逆时针排列并且法线指向多边形内部,那么我们能不能像凸多边形一样,依次判断点是否在每条边的正面来判断多边形是否包含这个点呢?让我们试试吧,首先对于边A,如果点在A的负面表示点不在多边形内,否则在A的正面表示点可能在多边形内部,需要继续跟下一条边判断,到边B的时候,如果点在B的负面,能不能表示点不在多边形内部呢? 其实是不能的,因为一个点在边B的负面,但是有可能在边D的正面,所以说凹多边形不能用凸多边形的点包含判断算法。
那么对于凹多边形,是怎么来判断它是否包含一个点呢?在3D室内游戏中,有个比较经典的算法叫BSP,即二元空间分割算法。用BSP对这个凹多边形分割后,就能很轻松地判断一个点在不在BSP内了。我们先在2D这么一个比较简单的环境下介绍BSP算法,然后再讲一下它的第一个简单应用,即点的包含判断算法。 BSP是把凹多边形的每条边的直线都作为一个分割直线,把空间一分为二,一个是在直线正面的正空间,一个是在直线负面的负空间。 一直分割到没有边可分割为止。 而选择一个边作为分割线的时候要遵循它截断的其他边数最少,并且分割后,空间两边的边的数量都趋于平衡。
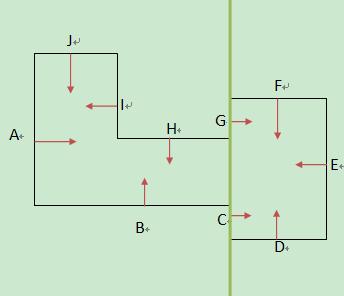
对于上面的凹多边形,我们首先选择边C来进行分割,当然由于边G也在边C的分割直线上,所以它在作为这个分割节点的内部边,我们来看看由这个分割线分割后的结果:
 =>
=> +
+
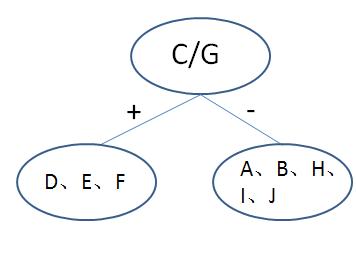
如上所示,在C、G边的直线分割后,凹多边形变成了由 A、B、H、I、J组成的负面,以及由D、E、F组成的正面。我们可以看节点树的图:
对于正面,由于已经成为了凸多边形的了,所以随便选择一条边做分割即可,按边的顺序所以我们选择边D来作为分割线; 而对于负面,按照最少截断的方案,我们先选择边A作为分割线,于是分割后的结果如下:
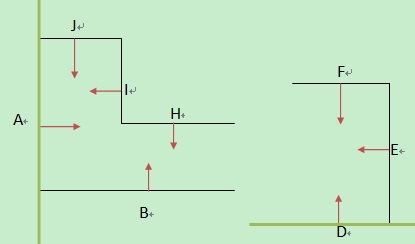
如上图,对空间再次分割后,C/G的正半空间还剩E和F的边,而负半空间剩下B、H、I、J四条边。然后我们对正负两个子树继续分割:


如上图,我们对正半空间分割,由于只有E、F两条边了,所以我们随意选择一条边作为分割直线,根据顺序我们选择E边作为这一次的分割边。而对于负半空间,我们根据分割两边的边的数量的趋于平衡的原则选择H边作为分割直线,于是它的正半空间剩下B边,而负半空间还剩下I和J两条边。对于负半空间最后的I、J,我们也是按顺序选择了I边作为分割边,于是最后的分割结果如下:
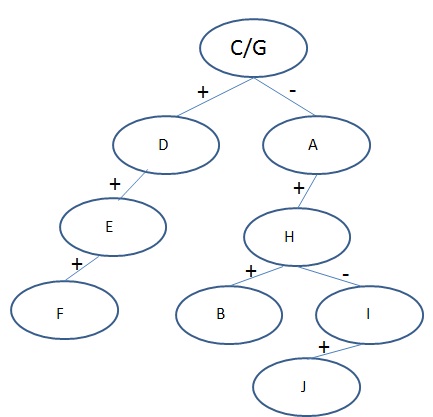
这样我们整个凹多边形就分割完毕了。让我们来看看怎么判断一个点在不在这个凹多边形内。 首先这个点将套用C、G组成的直线的基本公式,看是在C、G直线的正半空间还是负半空间。如果在正半空间的话,就继续套用由边D构成的直线的基本公式,看是在D直线的正半空间还是负半空间,如果是在D直线的负半空间,而D负半空间又没有子节点了,就表示点不在这个凹多边形里面。 如果在正半空间的话,则继续判断D的正子树E构成的直线。一直检测到没有负子树的节点的负半空间则表示点不在凹多边形内,或者检测到没有正子树的节点的正半空间则表示点在凹多边形内。
所以对于这个由A到J共10条边构成的凹多边形,检测是否包含点的时候,需要套用直线定义公式2到5遍。
现在差不多是要到了写代码的时候,首先我们定义了一个直线类:
// 点是在直线的哪边?
enum EPointLineSide
{
POINT_LINE_SIDE_FRONT, // 点在直线的前面
POINT_LINE_SIDE_IN, // 点在直线上
POINT_LINE_SIDE_BEHIND, // 点在直线的后面
};
// 线段是在直线的哪边?
enum ESegmentLineSide
{
SEGMENT_LINE_SIDE_FRONT, // 线段在直线的前面
SEGMENT_LINE_SIDE_COLLINEAR, // 线段在直线上
SEGMENT_LINE_SIDE_BEHIND, // 线段在直线的后面
SEGMENT_LINE_SIDE_STRADDLING, // 线段和直线交叉
};
// 线段类前向申明
class LineSegment2d;
// 直线类
class Line2d
{
public:
// 默认构造
Line2d() : m_normal(0.f, 0.f), m_d(0.f) {}
// 用直线的两个点来构造
Line2d(const Vector2 &p1, const Vector2 &p2);
// 判断点是在直线的哪边
EPointLineSide ClassifyPoint(const Vector2 &pos);
// 判断线段在直线的哪边
ESegmentLineSide ClassifySegment(const LineSegment2d &seg);
Vector2 m_normal; // 直线的法线
float m_d; // 直线的d
};
大家注意这里有两个函数, 一个是ClassifyPoint即判断一个点是在这条直线的正面还是负面或者是在直线上。第二个是ClassifySegment,即判断一个线段是在这条直线的正面还是负面或者在直线上,或者是被这条直线截断为两半了。
然后我们再看看线段类的定义:
// 计算两个直线的交点
bool IntersectionLines(const Line2d &l1, const Line2d &l2, Vector2 &out);
// 线段类
class LineSegment2d
{
public:
// 默认构造
LineSegment2d() { }
// 用两个端点来构造
LineSegment2d(const Vector2 &p1, const Vector2 &p2){ m_vers[0] = p1; m_vers[1] = p2; }
// 获取这个线段对应的直线
Line2d GetLine() const { return Line2d(m_vers[0], m_vers[1]); }
// 获取顶点,索引0为顶点1,索引1为顶点2
const Vector2& GetVertex(int i) const;
Vector2 m_vers[2];
};
// 用一条直线把一个线段分成两段分别输出到frontSeg和backSeg
void SplitLineSegment(const LineSegment2d &seg, Line2d line, LineSegment2d &frontSeg, LineSegment2d &backSeg);
那么我们的基础类都定义好了,让我们看看最核心的BSP类吧:
// 2D的BSP树的节点
struct TBspNode2d
{
Line2d line; // 分割直线
vector<LineSegment2d> segs; // 这个节点的线段数组
TBspNode2d *front; // 前向子节点
TBspNode2d *behind; // 后向子节点
TBspNode2d *parent; // 父节点
TBspNode2d() { front = 0; behind = 0; parent = 0; }
TBspNode2d(Line2d l, TBspNode2d *f, TBspNode2d *b, TBspNode2d *p) { line = l; front = f; behind = b; parent = p; }
void clear() { segs.clear(); front = 0; behind = 0; parent = 0; }
};
以上是BSP节点的结构,下面是BSP类:
// 2D的BSP树
class BspTree2d
{
public:
BspTree2d() { m_Root = NULL; }
~BspTree2d() { DestroyNodes(m_Root); }
// 销毁BSP树的递归函数
void DestroyNodes(TBspNode2d *node);
// 构建BSP树的递归函数
TBspNode2d *BuildBspTree(vector<LineSegment2d> &segs, int depth = 0, TBspNode2d *parent = 0);
// 是否包含某点
bool IsContainPoint(Vector2 pos, TBspNode2d *node = 0);
// 选择一个最佳分割直线
Line2d PickSplittingLine(vector<LineSegment2d> &segs);
TBspNode2d *m_Root; // 这个BSP树的根节点
};
以上是BSP数的类定义,有两个函数比较重要,一个是BuildBspTree,通过一个线段列表来构建一颗BSP数。另一个是IsContainPoint函数,在一个构建好的BSP树上判断一个点在不在这个BSP空间之内。下面让我们分别看看这两个函数的实现。
// 构建BSP树的递归函数
TBspNode2d * BspTree2d::BuildBspTree(vector<LineSegment2d> &segs, int depth /* = 0 */, TBspNode2d *parent /* = 0 */)
{
// 如果已经没有边分割了,则返回NULL
if (segs.empty())
{
return NULL;
}
// 获取剩余的边数
size_t iNumSegs = segs.size();
// 如果是最后一条边了,则构造这个叶子节点
if (iNumSegs == 1)
{
return new TBspNode2d(segs[0].GetLine(), segs, parent);
}
// 选择一个最佳分割直线
Line2d splitLine = PickSplittingLine(segs);
vector<LineSegment2d> frontList; // 直线前面的线段列表
vector<LineSegment2d> backList; // 直线后面的线段列表
vector<LineSegment2d> inList; // 在直线上的线段列表
// 对于每个剩余的边
for (size_t i=0; i<iNumSegs; ++i)
{
LineSegment2d &seg = segs[i];
LineSegment2d frontPart;
LineSegment2d backPart;
// 看这条边在分割直线的哪边
ESegmentLineSide eLineSide = splitLine.ClassifySegment(seg);
switch (eLineSide)
{
case SEGMENT_LINE_SIDE_COLLINEAR: // 如果这条边在分割直线上
inList.push_back(seg);
break;
case SEGMENT_LINE_SIDE_FRONT: // 如果这条边在分割直线的前面
frontList.push_back(seg);
break;
case SEGMENT_LINE_SIDE_BEHIND: // 如果这条边在分割直线的后面
backList.push_back(seg);
break;
case SEGMENT_LINE_SIDE_STRADDLING: // 如果这条边被分割直线截断成两段了
SplitLineSegment(seg, splitLine, frontPart, backPart);
frontList.push_back(frontPart);
backList.push_back(backPart);
break;
}
}
// 构建这个BSP节点
TBspNode2d *pCurrNode = new TBspNode2d(splitLine, inList, parent);
// 递归构建这个BSP节点的前子树
pCurrNode->front = BuildBspTree(frontList, depth+1, pCurrNode);
// 递归构建这个BSP节点的后子树
pCurrNode->behind = BuildBspTree(backList, depth+1, pCurrNode);
// 如果是第0层的,则为根节点,赋一下值
if (depth == 0 && m_Root == 0)
{
m_Root = pCurrNode;
}
// 返回当前BSP节点
return pCurrNode;
}
以上函数是从一个线段列表中递归构建BSP的主函数,它调用了PickSplittingLine,这个函数是用来在线段列表中选择一条边的直线作为最佳的分割直线。它的原理大概是这样,选择一条截断其他边数最少,并且分割两边的边数趋于平衡的直线作为分割直线。
构建好BSP树后,我们可以判断一个点在不在BSP的多边形内了,让我们看看IsContainPoint函数的实现吧:
// 是否包含某点
bool BspTree2d::IsContainPoint(Vector2 pos, TBspNode2d *node /* = 0 */)
{
if (node == NULL)
{
node = m_Root;
}
EPointLineSide eLineSide = node->line.ClassifyPoint(pos);
// 判断在直线的那边
switch (eLineSide)
{
// 如果在直线上
case POINT_LINE_SIDE_IN:
// 如果在直线的正面
case POINT_LINE_SIDE_FRONT:
if (node->front)
{
// 递归调用前子树来判断
return IsContainPoint(pos, node->front);
}
// 否则没有前子树了,则返回真,表示包含这个点
return true;
break;
// 如果在直线的后面
case POINT_LINE_SIDE_BEHIND:
if (node->behind)
{
// 递归调用后子树来判断
return IsContainPoint(pos, node->behind);
}
// 否则没有后子树了,则返回假,表示不包含这个点
return false;
break;
}
return false;
}
这样我们就可以判断一个点在不在BSP所代表的多边形内了。
完整的代码可以从以下网址下载:
http://download.csdn.net/source/3549437
它在VC++2005编译通过。