这是学习bingshangjiguang大神的算法,记录如下。
RMQ问题:
Range Minimum/Maximum Query问题,给定一个区间,求这个区间的最大值或最小值,需要采用动态规划的思想。
举例:
以求最小值为例:f(i, j)表示[i,i+2^j-1]区间中的最小值。i表示起点,j近似表示区间的长度。例如:f(0,0)就表示[0,0]之间的最小值,f(0,2)表示[0,2]之间的最小值,f(2,17)表示[2,2+2^17-1]之间的最小值。
性质:
1.f(i, j) = min( f(i, j-1), f(i + 2^(j - 1) , j - 1)推到得出。也就是把一段线段分成了两个等长的子线段。
2.f(i,0)已知。
DP策略: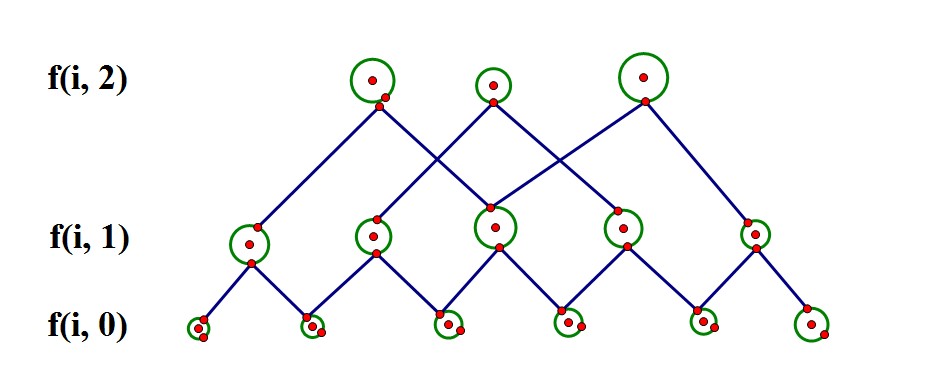
自底而上求得,所有符合条件的f(i, j)的值,即先求f(i,1)i =0, 1, 2, 3, 4 ……再求f(i, 2) i = 0, 1, 2, 3, ……
取值范围:
1.设有p个点,那么总体上0<=i<=p-1;0<=j<=log2(p);
2.同时对于第k层,即当j = k时候;i = [0,p-1] (k == 0) ; i = [0,p-1-2^(k-1)] (k != 0);
查询:
假设要查询从m到n这一段的最小值,那么我们先找出一个最大的k,满足k满足2^k<=(n-m+1);
那么我们就可以把[m,n]分成两个(部分重叠的)长度为2^k的区间:[m,m+2^k-1],[n-2^k+1,n]
复杂度:
1.初始化:设有n个点,那么g(n) = n + n/2 + n / 2 / 4 + n / 2 / 4/ 8 ,复杂度求法:n < g(n) < n + n/2 + n / 4 + n / 8 + n / 16 + …… < 2*n;所以复杂度为O(n);
2.查询:O(1)
例题:
poj3264
/*
下一个代码写递归的形式
*/
#include<iostream>
#include<math.h>
#include<cstdlib>
#include<algorithm>
#include<cstring>
#include<cstdio>
using namespace std;
int mat_min[50100][20];
int mat_max[50100][20];
int seq[50100];
int N, Q;
#define chmin(a,b) ((a)<(b)?(a):(b))
#define chmax(a,b) ((a)>(b)?(a):(b))
void initial()
{
//初始化不能通过传参进行
memset(mat_max, 0, sizeof(mat_max));
memset(mat_min, 0, sizeof(mat_min));
}
void initial_mat()
{
for(int i = 0; i < N; i++) mat_max[i][0] = mat_min[i][0] = seq[i];
for(int j = 1; j <= log(N * 1.0 + 1) / log(2.0); j++)//此处会不会有精度问题
{
for(int i = 0; i < N - (1<<j) + 1; i++)
{
mat_max[i][j] = chmax(mat_max[i][j - 1], mat_max[i + (1<<(j - 1))][j - 1]);
mat_min[i][j] = chmin(mat_min[i][j - 1], mat_min[i + (1<<(j - 1))][j - 1]);
}
}
return ;
}
/*
//更加通俗表示为1<<power.例外power = 0
int poww(int base, int power)
{
int ret = 1;
int tmp = power;
while(power--) ret *= base;
return ret;
}
*/
int find_k(int m, int n)
{
int ret = 1;
while((1<<ret) < (n - m + 1)) ret++;
return ret - 1;
}
void find_max_min(int begin, int end, int& max, int& min)
{
//int k = log(end - begin + 1) / log(2.0);//转换成以2为底
if(begin == end)
{
max = mat_max[begin][0];
min = mat_min[begin][0];
}
else
{
int k = find_k(begin, end);
//cout<<"k="<<k<<" begin="<<begin<<" end="<<end<<endl;
//cout<<"mat_max[begin][k]="<<mat_max[begin][k]<<endl;
//cout<<"mat_max[end - 2 ^ k + 1][k]="<<mat_max[end - 2 ^ k + 1][k]<<endl;
max = chmax(mat_max[begin][k], mat_max[end - (1<<k) + 1][k]);
min = chmin(mat_min[begin][k], mat_min[end - (1<<k) + 1][k]);
}
return ;
}
void input_data()
{
cin>>N>>Q;
for(int i = 0; i < N; i++) scanf("%d", &seq[i]);
return ;
}
void debug()
{
for(int j = 0; j <= log(N + 1.0) / log(2.0); j++)
{
for(int i = 0; i < N; i++)
{
//cout<<i<<" "<<i + (1<<j)<<" "<<mat_max[i][j]<<endl;
cout<<i<<" "<<j<<" "<<mat_max[i][j]<<endl;
}
}
}
int main()
{
input_data();
initial_mat();
//debug();
//system("pause");
for(int i = 0; i < Q; i++)
{
int begin, end;
scanf("%d%d", &begin, &end);
int maxx, minn;
begin--;
end--;
find_max_min(begin, end, maxx, minn);
//cout<<maxx<<" "<<minn<<endl;
cout<<maxx - minn<<endl;
}
return 0;
}
这是代码,曾有的bug:
1.^符号在C++中是异或运算,在平时书写时是取幂,不能混淆。
2.code过程中可能数组是从0开始的,但是输入数据是从1开始的,所以begin--, end--。
神牛的code:
#include<cstdio>
#include<cmath>
#include<algorithm>
using namespace std;
int f[50005],p[50005][20],q[50005][20],i,j,k,n,nq,a,b,sa,ya,t;
int main()
{
scanf("%d%d",&n,&nq);
for (i=1;i<=n;i++) {scanf("%d",&f[i]);p[i][0]=f[i];q[i][0]=f[i];}
for (j=1;j<=log((double)(n+1))/log(2.0);j++)
for (i=1;i+(1<<j)-1<=n;i++)
{
p[i][j]=min(p[i][j-1],p[i+( 1<<(j-1) )][j-1]);
q[i][j]=max(q[i][j-1],q[i+( 1<<(j-1) )][j-1]);
}
while(nq--)
{
scanf("%d%d",&a,&b);
k=(int)(log((double)(b-a+1))/log(2.0));
printf("%d\n", max( q[a][k],q[b-(1<<k)+1][k]) - min( p[a][k], p[b-(1<<k)+1][k] ) ) ;
}
}
