转自：http://en.wikipedia.org/wiki/First-countable_space

First-countable space

In topology,
a branch of mathematics,
a first-countable space is a topological
space satisfying the "first axiom
of countability". Specifically, a space X is
said to be first-countable if each point has a countable neighbourhood
basis (local base). That is, for each point x in X there
exists a sequence U₁, U₂,
… of open
neighbourhoods of x such
that for any open neighbourhood V of x there
exists an integer i with U_i contained
in V.

转自：http://en.wikipedia.org/wiki/Second-countable_space

Second-countable space

In topology,
a second-countable space, also called a completely
separable space, is a topological
space satisfying the second axiom
of countability. A space is said to be second-countable if its topology has a countable base.
More explicitly, this means that a topological space 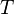is
second countable if there exists some countable collection 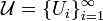 of
open subsets of 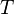 such
that any open subset of 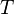 can
be written as a union of elements of some subfamily of .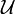
Like other countability axioms, the property of being second-countable restricts the number of open
sets that a space can have.

Most "well-behaved"
spaces in mathematics are
second-countable. For example, Euclidean space (Rⁿ)
with its usual topology is second-countable. Although the usual base of open
balls is not countable, one can restrict to the set of all open balls with rational radii
and whose centers have rational coordinates. This restricted set is countable and still forms a basis.