“齐次坐标表示是计算机图形学的重要手段之一,它既能够用来明确区分向量和点,同时也更易用于进行仿射(线性)几何变换。”
—— F.S. Hill, JR。
在学习3D图形学最初遇到的问题就是难以理解的概念和复杂的数学推导流程,齐次坐标就是其中之一。
齐次坐标主要是应用在矩阵转换中,我们通常运算的坐标系是“笛卡尔坐标系”,我们已经习惯了笛卡尔坐标系的表述方式,一个点都有唯一对应的数据值来表示,比如原点我们就记做(0,0)点。而笛卡尔坐标系和齐次坐标系的根本区别在于“齐次性”。
所谓齐次坐标就是将一个原本是n维的向量用一个n+1维向量来表示。 显然一个向量的齐次表示是不唯一的,齐次坐标的h取不同的值都表示的是同一个点,比如齐次坐标[10,4,2]、[5,2,1]表示的都是二维点[5,2]。
那么引进齐次坐标有什么必要,它有什么优点呢?
由于[10,4,2]、[5,2,1]表示的都是[5,2]一个点,如果有一个公式需要将[5,2]点参与的运算3维运算,而我们的点只有2维的表示,那么我们在值不变的情况下增加一个齐次坐标,使之变成3维,而能够参加运算并不影响最终结果,这就是齐次坐标的价值。至于优点我们在后面的章节里慢慢说。
那么齐次坐标是怎么表示点和向量的呢?
那要从齐次坐标的线性代数性质来看:
一维齐次点坐标:
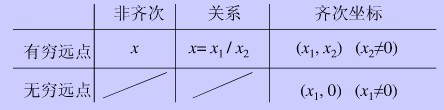
通过上面的定义可以看出,一维的点坐标x的值是齐次坐标中(x1,x2)的关系有 x = x1/x2; 如果x2=1,那么既可以表示为(x,1).其中最特别的点是(0,1)
如果有齐次坐标(x1,x2),由于x2=0的时候表达式分母为零,除法表达式失去意义,因此(x1,0)表示的是一个无穷远点。即忽略其长度属性,那么它就表示一个方向,其中最特别的是(1,0)。
对于 二维齐次点坐标:
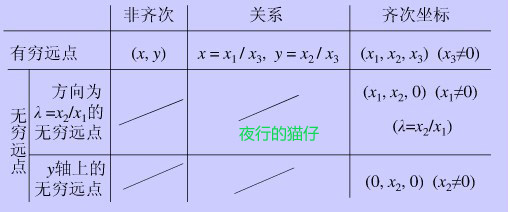
上图表达的意义就是一个点(x,y)他的齐次坐标就是(w*x,w*y,w)其中w不为0
下表列举了一些点的其次表示方式:

任意方向的无穷远点是(x1,x2,0)其中方向为x2/x1 y轴上的无穷远点的表示方式是(0,x2,0)。
在用向量的办法来看看 齐次坐标表示“向量“和“点”的区别。
对于一个向量v以及基oabc,可以找到一组坐标(v1,v2,v3),使得v = v1 a + v2 b + v3 c (1)
现在有一个点P,根据向量的性质,v=p-o (o是原点,v表示从坐标原心指向点p的向量) ,那么代入上式即可得到
p – o = p1 a + p2 b + p3c (2)
那么点 p的表达式就是 p = o + p1 a +
p2 b + p3 c (3) 那么就会发现,点p的表达式就要比向量v多一个信息。但是o也可以用三维向量来表述,所以
P(1,2,3)和V(1,2,3)从值上而言是完全没有区别的,所以点的就可以用(1,2,3,1)来表示,而向量是(1,2,3,0)。齐次坐标的w为0表示无穷远点,那就只能代表一个方向了。
