学步园

1、最长字符连接

有n个长为m+1的字符串，如果某个字符串的最后m个字符与某个字符串的前m个字符匹配，则两个字符串可以联接，问这n个字符串最多可以连成一个多长的字符串，如果出现循环，则返回错误。

分析：

将各个字符串作为一个节点，首尾链接就好比是一条边，将两个节点连接起来，于是问题就变成一个有关图的路径长度的问题。链接所得的字符串最长长度即为从图的某个节点出发所能得到的最长路径问题，与最短路径类似，可以应用弗洛伊德算法求解。对于循环，即可认为各个节点通过其他节点又回到自己，反应在路径长度上，就表示某个节点到自己节点的路径大于零（注：初始化个节点到自己的长度为零）。

弗洛伊德算法介绍

Floyd-Warshall算法（Floyd-Warshall algorithm）是解决任意两点间的最短路径的一种算法，可以正确处理有向图或负权的最短路径问题，同时也被用于计算有向图的传递闭包。Floyd-Warshall算法的时间复杂度为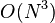，空间复杂度为。

Floyd-Warshall算法的原理是动态规划。

设为从到的只以集合中的节点为中间节点的最短路径的长度。

1. 若最短路径经过点k，则；
2. 若最短路径不经过点k，则。

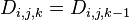因此，。

算法如下：

const int MAX = 1000000000;
int floyd(int matrix[5][5],int n)
{
 int dist[5][5];
 int path[5][5];
 for(int i=0; i<n; i++)
  for(int j=0; j<n; j++)
   dist[i][j] = matrix[i][j],path[i][j] = -1;
 for(int k=0; k<n; k++)
  for(int i=0; i<n; i++)
   for(int j=0; j<n; j++)
    if(dist[i][j]>dist[i][k]+dist[k][j])
     dist[i][j] = dist[i][k]+dist[k][j],path[i][j] = k;
 for(int i=0; i<n; i++)
 {
  for(int j=0; j<n; j++)
  {
   if(i!=j&&dist[i][j] != MAX)
   { 
    cout<<i<<"到"<<j<<"最短距离为"<<dist[i][j]<<endl;
    cout<<"路径逆序为:"<<j<<"->";
    int mid = path[i][j];
    while(mid!=-1)
     cout<<mid<<"->",mid = path[i][mid];
    cout<<i<<endl<<endl;
   }
  }
 }
 return 0;   
}
int _tmain(int argc, _TCHAR* argv[])
{
 int matrix[5][5] = {0,MAX,1,4,MAX,
  MAX,0,MAX,MAX,MAX,
  MAX,MAX,0,MAX,2,
  MAX,3,MAX,0,MAX,
  MAX,3,MAX,MAX,0};
 floyd(matrix,5);
 return 0;
}

运行如下：

问题代码如下：

void maxLengthInStrings(string text[],int nSize)
{
int dist[100][100];
int path[100][100];
memset(path,-1,sizeof(int)*100*100);
memset(dist,0,sizeof(int)*100*100);
int m = text[0].size()-1;
for(int i=0; i<nSize; i++)
{
string iText = text[i].substr(1,m);
for(int j=0; j<nSize; j++)
{
if(i!=j)
{
string jText = text[j].substr(0,m);
if(iText == jText)
dist[i][j] = 1;
else 
dist[i][j] = 0;
}
}
}
for( int k=0; k<nSize; k++)
for( int i=0; i<nSize; i++)
for( int j=0; j<nSize; j++)
{
if(dist[i][k]&&dist[k][j])
{
if(dist[i][j]<dist[i][k]+dist[k][j])
{
dist[i][j] = dist[i][k]+dist[k][j];
path[i][j] = k;
}
}
}

int max_from,max_to,max = 0;
for(int i=0; i<nSize; i++)
{
for(int j=0; j<nSize; j++)
if(max<dist[i][j])
max = dist[i][j],max_from = i,max_to = j;
}
cout<<"最长串逆序如下"<<text[max_to]<<" ";
int mid = path[max_from][max_to];
while(mid>=0)
cout<<text[mid]<<" ",mid = path[max_from][mid];
cout<<text[max_from]<<endl;
}

// test

int _tmain(int argc, _TCHAR* argv[])
{
string text[] = { "abcd",  
                  "bcde",  
                   "cdea",  
                    "deab",  
                     "eaba",  
                      "abab",  
                    "deac",  
                   "cdei",  
                  "bcdf",  
                   "cdfi",  
                    "dfic",  
                   "cdfk",  
                  "bcdg",  
};
maxLengthInStrings(text,sizeof(text)/sizeof(text[0]));
return 0;
}

 运行结果如下：

 2、.用天平（只能比较，不能称重）从一堆小球中找出其中唯一一个较轻的，
使用x 次天平，最多可以从y 个小球中找出较轻的那个，求y 与x 的关系式

 三叉树，每次分为三等分，y = 3^x

3、随机数问题