http://blog.csdn.net/wumuzi520/article/details/7014830#reply
完全背包是在N种物品中选取若干件(同一种物品可多次选取)放在空间为V的背包里,每种物品的体积为C1,C2,…,Cn,与之相对应的价值为W1,W2,…,Wn.求解怎么装物品可使背包里物品总价值最大。
动态规划(DP):
1) 子问题定义:F[i][j]表示前i种物品中选取若干件物品放入剩余空间为j的背包中所能得到的最大价值。
2) 根据第i种物品放多少件进行决策
![]() (2-1)
(2-1)
其中F[i-1][j-K*C[i]]+K*W[i]表示前i-1种物品中选取若干件物品放入剩余空间为j-K*C[i]的背包中所能得到的最大价值加上k件第i种物品;
设物品种数为N,背包容量为V,第i种物品体积为C[i],第i种物品价值为W[i]。
与01背包相同,完全背包也需要求出NV个状态F[i][j]。但是完全背包求F[i][j]时需要对k分别取0,…,j/C[i]求最大F[i][j]值,耗时为j/C[i]。那么总的时间复杂度为O(NV∑(j/C[i]))
由此写出伪代码如下:
F[0][] ← {0}
F[][0] ← {0}
for i←1 to N
do for j←1 to V
do for k←0 to j/C[i]
if(j >= k*C[i])
then F[i][k] ← max(F[i][k],F[i-1][j-k*C[i]]+k*W[i])
return F[N][V]
以上伪代码数组均为基于1索引,即第一件物品索引为1。空间复杂度O(VN)、时间复杂度为O(NV∑(j/C[i]))
简单优化:
若两件物品满足C[i] ≤C[j]&&W[i] ≥W[j]时将第j种物品直接筛选掉。因为第i种物品比第j种物品物美价廉,用i替换j得到至少不会更差的方案。
这个筛选过程如下:先找出体积大于背包的物品直接筛掉一部分(也可能一种都筛不掉)复杂度O(N)。利用计数排序思想对剩下的物品体积进行排序,同时筛选出同体积且价值最大的物品留下,其余的都筛掉(这也可能一件都筛不掉)复杂度O(V)。整个过程时间复杂度为O(N+V)
转化为01背包:
因为同种物品可以多次选取,那么第i种物品最多可以选取V/C[i]件价值不变的物品,然后就转化为01背包问题。整个过程的时间复杂度并未减少。如果把第i种物品拆成体积为C[i]×2k价值W[i]×2k的物品,其中满足C[i]×2k≤V。那么在求状态F[i][j]时复杂度就变为O(log2(V/C[i]))。整个时间复杂度就变为O(NVlog2(V/C[i]))
时间复杂度优化为O(NV)
将原始算法的DP思想转变一下。
设F[i][j]表示出在前i种物品中选取若干件物品放入容量为j的背包所得的最大价值。那么对于第i种物品的出现,我们对第i种物品放不放入背包进行决策。如果不放那么F[i][j]=F[i-1][j];如果确定放,背包中应该出现至少一件第i种物品,所以F[i][j]种至少应该出现一件第i种物品,即F[i][j]=F[i][j-C[i]]+W[i]。为什么会是F[i][j-C[i]]+W[i]?因为F[i][j-C[i]]里面可能有第i种物品,也可能没有第i种物品。我们要确保F[i][j]至少有一件第i件物品,所以要预留C[i]的空间来存放一件第i种物品。
状态方程为:
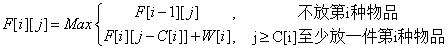 (2-2)
(2-2)
伪代码为:
F[0][] ← {0}
F[][0] ← {0}
for i←1 to N
do for j←1 to V
F[i][j] ← F[i-1][j]
if(j >= C[i])
then F[i][j] ← max(F[i][j],F[i][j-C[i]]+ W[i])
return F[N][V]
具体背包中放入那些物品的求法和01背包情况差不多,从F[N][V]逆着走向F[0][0],设i=N,j=V,如果F[i][j]==F[i][j-C[i]]+W[i]说明包里面有第i件物品,同时j -= C[i]。完全背包问题在处理i自减和01背包不同,01背包是不管F[i][j]与F[i-1][j-C[i]]+W[i]相不相等i都要减1,因为01背包的第i件物品要么放要么不放,不管放还是不放其已经遍历过了,需要继续往下遍历而完全背包只有当F[i][j]与F[i-1][j]相等时i才自减1。因为F[i][j]=F[i-1][j]说明背包里面不会含有i,也就是说对于前i种物品容量为j的背包全部都放入前i-1种物品才能实现价值最大化,或者直白的理解为前i种物品中第i种物品物不美价不廉,直接被筛选掉。
打印背包内物品的伪代码如下:
i←N
j←V
while(i>0 && j>0)
do if(F[i][j]=F[i][j-C[i]]+W[i])
then Print W[i]
j←j-C[i]
else
i←i-1
和01背包一样,也可以利用一个二维数组Path[][]来标记背包中的物品。开始时Path[N][V]初始化为0,当 F[i][j]==F[i][j-C[i]]+W[i]时Path[i][j]置1。最后通过从Path[N+1][V+1]逆着走向Path[0][0]来获取背包内物品。其中Path[0][]与Path[][0]为边界。同样,在打印路径的时候当Path[][]=1时,打印W[i];Path[][]=0时i自减1.
加入路径信息的伪代码如下:
F[0][] ← {0}
F[][0] ← {0}
Path[][] ← 0
for i←1 to N
do for k←1 to V
F[i][k] ← F[i-1][k]
if(k >= C[i] && F[i][k] < F[i][k-C[i]]+W[i])
then F[i][k] ← F[i][k-C[i]]+W[i]
Path[i][k] ← 1
return F[N][V] and Path[][]
打印背包内物品的伪代码如下:
i←N
j←V
while(i>0 && j>0)
do if(Path[i][j]=1)
then Print W[i]
j←j-C[i]
else
i←i-1
优化空间复杂度为O(V)
和01背包问题一样,完全背包也可以用一维数组来保存数据。算法样式和01背包的很相似,唯一不同的是对V遍历时变为正序,而01背包为逆序。01背包中逆序是因为F[i][]只和F[i-1][]有关,且第i件的物品加入不会对F[i-1][]状态造成影响。而完全背包则考虑的是第i种物品的出现的问题,第i种物品一旦出现它势必应该对第i种物品还没出现的各状态造成影响。也就是说,原来没有第i种物品的情况下可能有一个最优解,现在第i种物品出现了,而它的加入有可能得到更优解,所以之前的状态需要进行改变,故需要正序。
状态方程为:
 (2-3)
(2-3)
伪代码如下:
F[] = {0}
for i←1 to N
do for k←C[i] to V
F[k] ← max(F[k],F[k-C[i]]+W[i])
return F[V]
具体背包中放入那些物品的求法和上面空间复杂度为O(NV)算法一样,用一个Path[][]记录背包信息。但这里面是当F[i]=F[i-C[i]]+W[i]时将Path置1.
伪代码如下:
F[0][] = {0}
F[][0] = {0}
Path[][] ← 0
for i←1 to N
do for k←C[i] to V
if(F[i] < F[k-C[i]]+W[i])
then F[i] ← F[k-C[i]]+W[i]
Path[i][k] ← 1
return F[N][V] and Path[][]
打印路径的伪代码和前面未压缩空间复杂度时的伪代码一样,这里不再重写。
举例:表2-1为一个背包问题数据表,设背包容量为10根据上述解决方法可得到对应的F[i][j]如表2-2所示,最大价值即为F[6][10].
表2-1背包问题数据表
| 物品号i | 1 | 2 | 3 | 4 | 5 | 6 |
| 体积C | 3 | 2 | 5 | 1 | 6 | 4 |
| 价值W | 6 | 5 | 10 | 2 | 16 | 8 |
表2-2前i件物品选若干件放入空间为j的背包中得到的最大价值表
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 6 | 6 | 6 | 12 | 12 | 12 | 18 | 18 |
| 2 | 0 | 0 | 5 | 6 | 10 | 11 | 15 | 16 | 20 | 21 | 25 |
| 3 | 0 | 0 | 5 | 6 | 10 | 11 | 15 | 16 | 20 | 21 | 25 |
| 4 | 0 | 2 | 5 | 7 | 10 | 12 | 15 | 17 | 20 | 22 | 25 |
| 5 | 0 | 2 | 5 | 7 | 10 | 12 | 16 | 18 | 21 | 23 | 26 |
| 6 | 0 | 2 | 5 | 7 | 10 | 12 | 16 | 18 | 21 | 23 | 26 |
下面针对前面提到的表2-1提供两种方法的测试代码:
int Package02(int Weight[], int Value[], int nLen, int nCapacity)
{
int** Table = NULL;
int** Path = NULL;
CreateTwoDimArray(Table,nLen+1,nCapacity+1); //创建二维数组
CreateTwoDimArray(Path,nLen+1,nCapacity+1); //创建二维数组
for(int i = 1; i <= nLen; i++)
{
for(int j = 1; j <= nCapacity; j++)
{
Table[i][j] = Table[i-1][j];
if(j >= Weight[i-1] && Table[i][j] < Table[i][j-Weight[i-1]]+Value[i-1])
{
Table[i][j] = Table[i][j-Weight[i-1]]+Value[i-1];
Path[i][j]=1;
}
}
}
int i = nLen, j = nCapacity;
while(i > 0 && j > 0)
{
if(Path[i][j] == 1)
{
cout << Weight[i-1] << " ";
j -= Weight[i-1];
}
else
i--;
}
cout << endl;
int nRet = Table[nLen][nCapacity];
DestroyTwoDimArray(Table,nLen+1); //销毁二维数组
DestroyTwoDimArray(Path,nLen+1); //销毁二维数组
return nRet;
}
//时间复杂度O(VN),不考虑路径空间复杂度为O(V),考虑路径空间复杂度为O(VN)
int Package02_Compress(int Weight[], int Value[], int nLen, int nCapacity)
{
int * Table = new int [nCapacity+1];
memset(Table,0,(nCapacity+1)*sizeof(int));
int** Path = NULL;
CreateTwoDimArray(Path,nLen+1,nCapacity+1); //创建二维数组
for(int i = 0; i < nLen; i++)
{
for(int j = Weight[i]; j <=nCapacity; j++)
{
if(Table[j] < Table[j-Weight[i]]+Value[i])
{
Table[j] = Table[j-Weight[i]]+Value[i];
Path[i+1][j] = 1;
}
}
}
int i = nLen, j = nCapacity;
while(i > 0 && j > 0)
{
if(Path[i][j] == 1)
{
cout << Weight[i-1] << " ";
j -= Weight[i-1];
}
else
i--;
}
cout << endl;
int nRet = Table[nCapacity];
DestroyTwoDimArray(Path,nLen+1); //销毁二维数组
delete [] Table;
return nRet;
}
int main()
{
int Weight[] = {3,2,5,1,6,4};
int Value[] = {6,5,10,2,16,8};
int nCapacity = 10;
cout << Package02(Weight,Value,sizeof(Weight)/sizeof(int),nCapacity) << endl;
cout << Package02_Compress(Weight,Value,sizeof(Weight)/sizeof(int),nCapacity) << endl;
return 0;
}
本文部分内容参考“背包九讲”
以下是全部的代码:
#define N 6
#define W 21
int Value[N+1]={-1,3,2,5,1,6,4};
int Weight[N+1]={-1,6,5,10,2,16,8};
int Table[N+1][W+1];
int Path[N+1][W+1];
//初始的完全背包问题代码 未经任何优化
int Package02_0(int Weight[],int Value[])
{
for(int i=0;i<N+1;i++)
{
for(int j=0;j<W+1;j++)
{
Table[i][j]=-1;
Path[i][j]=0;
}
}
for(int i=0;i<N+1;i++)
Table[i][0]=0;
for(int j=0;j<W+1;j++)
{
Table[0][j]=0;
}
for(int i=1;i<N+1;i++)
{
for(int j=1;j<W+1;j++)
{
for(int k=0;k<=j/Weight[i];k++)
{
Table[i][j]=max(Table[i-1][j],Table[i][j]);
if(j>=k*Weight[i])
{
int t1=Table[i-1][j-k*Weight[i]]+k*Value[i];
int t2=Table[i][j];
Table[i][j]=t1>t2?t1:t2;
if(t1>t2)
Path[i][j]=1;
}
}
}
}
int i=N;
int j=W;
while(i>0&&j>0)
{
if(Path[i][j]==1)
{
cout<<Weight[i]<<" ";
j-=Weight[i];
}
else
i--;
}
cout<<endl;
return Table[N][W];
}
int Package02(int Weight[],int Value[])
{
for(int i=0;i<N+1;i++)
{
for(int j=0;j<W+1;j++)
{
Table[i][j]=-1;
Path[i][j]=0;
}
}
for(int i=0;i<N+1;i++)
Table[i][0]=0;
for(int j=0;j<W+1;j++)
{
Table[0][j]=0;
}
for(int i=1;i<N+1;i++)
{
for(int j=1;j<W+1;j++)
{
Table[i][j]=Table[i-1][j];
if(j>=Weight[i]&&Table[i][j]<Table[i][j-Weight[i]]+Value[i])
{
Table[i][j]=Table[i][j-Weight[i]]+Value[i];
Path[i][j]=1;//
}
}
}
int i=N;
int j=W;
while(i>0&&j>0)
{
if(Path[i][j]==1)
{
cout<<Weight[i]<<" ";
j-=Weight[i];
}
else
i--;
}
cout<<endl;
return Table[N][W];
}
int Table1[W+1];
int Path1[N+1][W+1];
int Package02_Compress(int Weight[],int Value[])
{
memset(Table1,0,sizeof(Table1)/sizeof(int));
for(int i=0;i<N+1;i++)
for(int j=0;j<W+1;j++)
Path1[i][j]=0;
for(int i=1;i<N+1;i++)
{
for(int j=Weight[i];j<W+1;j++)
{
if(Table1[j]<Table1[j-Weight[i]]+Value[i])
{
Table1[j]=Table1[j-Weight[i]]+Value[i];
Path[i][j]=1;
}
}
}
int i=N,j=W;
while(i>0&&j>0)
{
if(Path[i][j]==1)
{
cout<<Weight[i]<<" ";
j-=Weight[i];
}
else
i--;
}
cout<<endl;
return Table1[W];
}
int main()
{
cout<<Package02(Weight,Value)<<endl;
cout<<Package02_Compress(Weight,Value)<<endl;
cout<<Package02_0(Weight,Value)<<endl;
return 0;
}