对于最简单的常微分方程形式,y'=F(x,y)与y(x0)=y0,我们假定F(x,y)适当光滑,在一定的区间内进行求值。这里讲的是差分的方法,通过寻求一系列离散点求解近似解y1,y2,y3……下面的所有,以函数Y'=Y-2*X/Y,Y(0)=1为例。
1、Euler方法
最原始的Euler格式是用向前差商的方法推导的,Yn+1=Yn+h*F(Xn,Yn)。基于这个道理,我们如果将前面算过的两个值都利用起来,那么我们就可以得到两步Euler格式,Yn+1=Yn-1+2*h*F(Xn,Yn)。同样的,如果用向后差商的方法,我们就可以得到隐式Euler格式,Yn+1=Yn+h*F(Xn,Yn+1),这里要用到Yn+1的值。如果我们将两者进行综合,就可以得到Euler格式的预报校正系统,改进Euler格式,就是将前者的结果代入后者中进行校正检验。此外,我们还可以对这小段区间[Xn,Yn]进行二分法,Yn+1=Yn+h*F(Xn+1/2,Yn+h*F(Xn,Yn)/2),从而得到变形Euler格式。
既然有了方法,那就编程吧。
double Euler1(double x,double y,double h)//改进的欧拉格式
{
double y1=Euler3(x,y,h);
return y+(f(x,y)+f(x+h,y1))*h/2;
}
double Euler2(double x,double y,double h)//变形的欧拉格式
{
double y1=y+f(x,y)*h/2;
return y+h*f(x+h/2,y1);
}
double Euler3(double x,double y,double h)//单步欧拉格式
{
return y+h*f(x,y);
}
double Euler4(double x,double y1,double y2,double h)//两步欧拉格式
{
return y1+2*h*f(x,y2);
}
经检验,得如下结果:
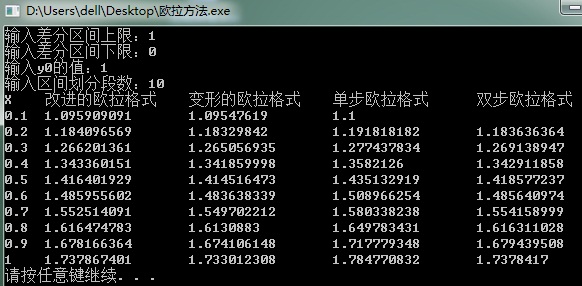
2、Runge-Kutta算法
由微分中值定理,我们知道存在Y'(ζ)=(Yn+1-Yn)/h,如何去寻找这个平均斜率呢?
Runge-Kutta给出了他们的方法,综合Euler格式的种种好处,利用均值的方法,我们有Yn+1=Yn+h*[F(Xn,Yn)+F(Xn+1,Yn+h*F(Xn,Yn))]/2:用单步Euler格式的结果再算得Y'n+1再与Y'n+1进行平均求得Yn+1的值,这便是一阶的Runge-Kutta。
为了达到更高的精度,再回首Euler格式,令K1=F(Xn,Yn),K2=F(Xn+p,Yn+p*h*K1),Yn+1=Yn+h*[(1-λ)K1+λK2],其中的p、λ都为待定系数。用Tylor展开式进行分析得,要使截断误差为o(h^3),则λ*p=0.5,这即为二阶的Runge-Kutta。当p=1、λ=0.5时为改进Euler格式,当p=0.5、λ=1时为变形Euler格式。
根据上面的原理,那如果我们再多加一个、两个待定系数呢?于是乎,我们可以得到三阶、四阶的Runge-Kutta公式。当然,在满足各自的条件下,我们常用以下两种。
三阶:K1=F(Xn,Yn),K2=F(Xn+1/2,Yn+h*K1/2),K3=F(Xn+1,Yn+h*(2*K2-K1)),Yn+1=Yn+h*[K1+4*K2+K3]/6。
四阶:K1=F(Xn,Yn),K2=F(Xn+1/2,Yn+h*K1/2),K3=F(Xn+1/2,Yn+K2*h/2),Yn+1=Yn+h*[K1+2*K2+2*K3+K4]/6。
有了这么多的理论支持,可以展开我们的编程了。
h=(b-a)/N;
R1[0]=y0;
x=a;
//一阶龙格库塔
for(int i=0;i<N;i++)
{
K1=F(x,R1[i]);
x+=h;
K2=F(x,R1[i]+h*K1);
R1[i+1]=R1[i]+(K1+K2)*h/2;
}
//二阶龙格库塔
R2[0]=y0;
x=a;
for(int i=0;i<N;i++)
{
K1=F(x,R2[i]);
x+=h/2;
K2=F(x,R2[i]+K1*h/2);
R2[i+1]=R2[i]+h*K2;
}
//三阶龙格库塔
R3[0]=y0;
x=a;
for(int i=0;i<N;i++)
{
K1=F(x,R3[i]);
x+=h/2;
K2=F(x,R3[i]+K1*h/2);
x+=h/2;
K3=F(x,R3[i]+h*(2*K2-K1));
R3[i+1]=R3[i]+h*(K1+4*K2+K3)/6;
}
//四阶龙格库塔
R4[0]=y0;
x=a;
for(int i=0;i<N;i++)
{
K1=F(x,R4[i]);
x+=h/2;
K2=F(x,R4[i]+K1*h/2);
K3=F(x,R4[i]+K2*h/2);
x+=h/2;
K4=F(x,R4[i]+h*K3);
R4[i+1]=R4[i]+(K1+2*K2+2*K3+K4)*h/6;
}
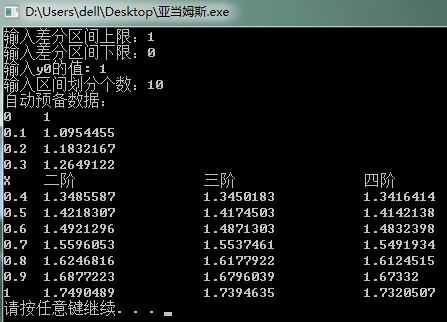
经验证,下面为差分结果:

3>Adams算法
Runge-Kutta已经很不错了,可是它在每一步前都要进行预报几个点以上的斜率值,计算量较为庞大。由于在计算Yn+1以前已经做过很多次计算了,那我们尝试利用以前的运算结果减少运算量。同样采用待定系数的思想,我们将目标向已经算过的地方看,经过分析,选取适当的系数,我们得到二阶、三阶、四阶等高精度的Adams算法。
二阶:Yn+1=Yn+(3*Y'n-Y'n-1)*h/2,预报校正Yn+1=Yn+(Y'n+1+Y'n)*h/2;
三阶:Yn+1=Yn+(23*Y'n-16*Y'n-1+5*Y'n-2)*h/12,预报校正Yn+1=Yn+(5*Y'n+1+8*Y'n-*Y'n-1)*h/12;
四阶:Yn+1=Yn+(55*Y'n-59*Y'n-1+37*Y'n-2-9*Y'n-3)*h/24,预报校正Yn+1=Yn+(9*Y'n+1+19*Y'n-5*Y'n-1+Y'n-2)*h/24。
有了公式,可以展开编程了。
//A[]用于存导数,0-1给二阶用,2-4给三阶用,5-8给四阶用。y[2]给二阶用,同理y[3]、y[4]
for(int i=0;i<N-3;i++)
{
//二阶亚当姆斯
y[0]=y[2];
y[2]=y[0]+(3*A[p2%2]-A[(p2-1)%2])*h/2;
p2++;
A[p2%2]=f(x+h,y[2]);
y[2]=y[0]+(A[p2%2]+A[(p2-1)%2])*h/2;
A[p2%2]=f(x+h,y[2]);
//三阶亚当姆斯
y[0]=y[3];
y[3]=y[0]+(23*A[p3]-16*A[p3%3+2]+5*A[(p3-1)%3+2])*h/12;
p3=(p3+1)%3+3;
if(p3==5)p3=2;
A[p3]=f(x+h,y[3]);
y[3]=y[0]+(5*A[p3]+8*A[p3%3+2]-A[(p3-1)%3+2])*h/12;
A[p3]=f(x+h,y[3]);
//四阶亚当姆斯
y[0]=y[4];
y[4]=y[0]+(55*A[p4]-59*A[(p4+2)%4+5]+37*A[(p4+1)%4+5]-9*A[p4%4+5])*h/24;
p4=(p4+1)%4+4;
if(p4==4)p4=8;
A[p4]=f(x+h,y[4]);
y[4]=y[0]+(9*A[p4]+19*A[(p4+2)%4+5]-5*A[(p4+1)%4+5]+A[p4%4+5])*h/24;
A[p4]=f(x+h,y[4]);
//结果输出比较
x+=h;
}
经验证,可得如下结果