学步园

　　前面§37中我们已经看到，两个射影相关的点列可以重叠在同一条直线上。其实，这种情况在两个射影相关的线束被一直线u所截时都会发生（参看下面的图47-1）。

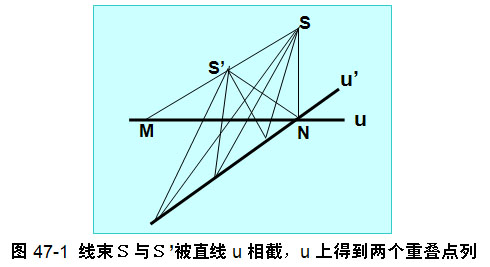
图中，S、S’是与同一透视轴u’ 透视相关的两个线束。直线u与这些射线相截，则直线u上就叠加了两个射影相关的点列，并且，我们立即能看出u和u’的交点N就是这两个射影相关点列一个自对应点。同时，u与线束中心S、S’的连线SS’的交点M也是一个自对应点。这个例子说明，两个叠加在同一直线上的射影相关点列可以有M、N两个自对应点。显然，如果两个线束中心的连线SS’通过u和u’的交点N时，自对应M就与N重合，自对应点就只有一个了。
　　类似地，两个射影相关的线束可以有一共同的中心。这种情况是在两个射影相关的点列u，u’同时投射到除透视中心S‘外的一个点S时发生的（参看图47-2）。

　　自然，对于两个射影相关的轴束，也可以有类似情形，即它们有相同的一个轴。总之，任何一种基本形在射影对应时都会有自对应元素。自对应元素的数目可能是一个，也可能是两个。在§37中我们已经看到，对于点列的情况，如果点B和D关于点A和C为调和共轭，则由B画出的点列射影对应于由D产生的点列，而A和C是自对应的点。

48. 射影对应的基本定理，连续性假设
　　上面我们已经证明，两个重迭在同一直线上的射影相关点列可以有一个自对应点，两个自对应点。现在我们来证明下面这个基本定理：
　　［定理］重迭在同一直线上的两个射影点列，如有两个以上的自对应点，则它们一定有无穷多个自对应点，且点列上每一个点都是自对应点，亦即两个点列完全重合。
　　［证明］设A，B，C是三个自对应点，则B关于A和C的调和共轭点D也是自对应点。（这是因为D的位置被A，B，C完全确定，A，B，C三个为自对应，对应后的位置不变，故D的位置也不变，所以D也是自对应点。）同样地可以说明，D关于B和C的调和共轭点E也必须对应于本身。这样，反复利用这种由三个老的自对应点来产生一个新的自对应点的办法，就可获得我们所希望多的无穷多自对应点。
　　下面我们进一步证明，直线上的任意一个点都是有限个或无穷多个自对应点的极限点。设 P为AB间的任意一个点，D是C对AB的第四调和点。D可能与P重合，这时序列为有限，结论得到证明；否则，P在区间AD或DB中。设P在DB间，作C关于D和B的第四调和点D’。D’也可能与P重合，这时，和前面一样，序列已找到。如果P在DD’间，作C关于DD’ 的第四调和点D’’，等等。这样，只要序列不结束，每走一步，P所允许的取值范围就减少一点。这一个过程可以无限继续，直到两个自对应点位于P的两旁，且与P的距离达到任意小。
　　我们这里显然利用了有关对应元素的连续性的基本假设。即，只要充分减少一个点列两点之间的距离，则其对应点列两点之间的距离也会任意减少。现设P不是自对应点，但对应于与P 有固定距离d的点P’。但如前一节所述，我们可以找到任意接近P的自对应点列，因此我们可以取到一点D，它与P可以任意接近，但D与P对应点D’和P’之间的距离只能趋近 d而不是零，这与连续性的假设矛盾。

49. 定理应用于线束和平面束.
　　我们可以把射影对应点列的上述结论应用到线束，即证明：具有同一透视中心的两个射影线束不可能有两个以上的自对应射线，除非它们是同一个线束。
　　［证明］用反证法。假设同一透视中心的两个射线束具有两个以上自对应直线。我们用一直线将射线束截断。这时在此直线上就得到了两个射影相关的点列，且它们有两个以上的自对应点，这不可能。
与此类似地，对于平面束，我们可证明：
　　具有同一轴线的两个射影相关平面束不可能有两个以上的自对应平面，除非它们是同一平面束。

50. 具有一公共自对应点的射影点列
　　现在来考察位于同一平面，但位于不同直线上两个射影相关的点列。它们的共同点可以是、也可以不是自对应点。如果两点列透视相关，则他们共同的点明显是自对应点。而且反之，也可证明它的非常重要的逆定理，如下：
　　［定理］在两个射影相关的点列中，如果交点对应到自己，则两个点列互为透视对应。
　　［证明］设两个点列为u和u’ (图50-1)，A与A’、B与B’是点列中对应的点，M是 u和u’的交点，且自对应。设AA’和BB’相交于点S，.以S为两个线束的中心，一个透视到u，另一透视到u’。这两个线束中，SA与对应射线SA’相重，SB 与对应射线SB’ 相重，SM与它对应的射线SM’相重，因此，由上节定理，两个线束相同，且所有射线SD必须与它对应的射线SD’重合，u和u’ 对应点都在通过S的直线上，故u和u’互为透视对应。

图50-1. 有自对应点M’的点列u,u’为透视对应

51. 无公共自对应点的射影相关点列
　　现在我们再考察，两个不同直线上没有自对应点的射影相关点列。这时有下面这一重要定理：
设u和u’是两个不同直线上没有自对应点的点列，A,B,C与A’,B’,C’分别是点列的对应点，则必存在两个透视对应，将A,B,C对应到A’,B’,C’，也就是使u射影对应到u’。
　　[证明] 设给定u和u’上的对应点A,B,C与A’,B’,C’。 如图51-1所示。我们按下列步骤具体找出这两个透视对应：

１）首先，连A与A’，并在AA’连线上任取一点S。２）通过A’任意作一条直线u”；３）以S为透视中心，把ABC投影到u”上，成为A”,B”,C”，其中A”与A’重合，为自对应点；４）将u”上的B”,C”与u’上B’,C’分别相连，连线交于Ｓ’。因u”与u’除了B”,C”与B’,C’对应外，还有A’作为自对应点，故u”与u’也是透视对应。由此证明了u和u’上的射影相关点列A,B,C与A’,B’,C可以利用S和S’两次透视对应来实现对应。

52. 透视对应的两个射线束
　　前面是关于点列的射影对应的性质，完全类似，可以证明下面有关线束与线束的对应，证明留给读者去完成。
在两个射影对应的线束中，如连接它们中心的直线为自对应，则两个线束透视对应。（参见图52-1）

图52-1 有自对应射线SS’的线束S,S’为透视对应

53. 透视对应的面束（轴束）
　　类似地还可证：两个射影对应的平面束为透视，如果两轴构成一个平面为自对应平面。
以上这些基本定理今后将频繁使用。

54. 调和元素的射影相关性
　　§35证明了射影对应使调和元素变到调和元素，现在反过来证明，如果一个对应使调和元素变到调和元素，那么这个对应一定是射影对应，即包含调和元素的两个基本形射影相关。
　　先考察点列的情况。设ABCD和A’B’C’D’是u，u’上的两个调和点列。根据§51的证明，我们可找到一个射影对应f，使ABC三点对应到A’B’C’三点。设在此射影对应下，u上D点对应到u’上的D1。因ABCD为u上调和点列，f为射影对应，故由§35知，A’B’C’D1也是调和点列。但另一方面，根据假设，A’B’C’D’ 是调和点列，由此，根据调和点列第4点的唯一性，可知D1和D’相同。由此说明使ABCD对应到A’B’C’D’的对应就是f，而这是一个射影对应。
　　如果调和元素不是点列而是线束或面束，则可利用投影和截影的办法，根据点列的性质直接推出，详细证明留给读者。
　　[推论1] 线束绕其中心转动，则所得的新线束与转动前的线束为射影对应的。
　　 [证明] 由上述的定理，我们只要考察a,b,c,d四调和线旋转后所得的a’,b’,c’,d’仍为四调和线。但这很明显，因a,b,c,d同时绕S旋转一个角度后所得射线a’,b’,c’,d’相互间的夹角不变，而线束的调和与否只和其间的夹角有关，夹角不变，调和关系也不变。

图54-1 a,b,c,d绕S旋转后得到四条新射线

　　利用这个推论，我们得到另一个推论：
 　　[推论2] 两个重迭在同一直线上的射影相关点列可以没有任何自对应点。
　　［证明］首先，线束经过旋转后，每一条射线都与原来的射线相差一个固定角，所以对应射线不可能有重合。因此，在上面图54-1中，由调和线束a,b,c,d决定的线束与旋转后得到的那个线束也没有任何重合射线。由此，与这两个线束直接透视的点列也没有重合点。但这两个点列包含的四点A,B,C,D与A’,B’,C’,D’均为调和元素，因而可知，这两个点列射影相关。这样我们看到了没有共同元素的两个射影相关点列。
　　我们在前面§47中我们曾经证明，两个重迭在同一直线上的射影相关点列可以有1个或2个自对应点；后来在§48中我们又证明了，两个重迭在同一直线上的射影相关点列如果有3个自对应点，则它们一定有无穷多个自对应点，且两个点列完全重合。现在又有了推论２，有关两个重叠在同一直线上的射影相关点列的各种情况都清楚了。

55. 二阶点列
　　自然会提出这样的问题：两个不透视对应但射影对应的线束对应射线的交点的轨迹是什么？这种轨迹将在随后的章节中详细讨论，它与平面上任意直线最多只有两个公共交点。按照这一特性，称这种轨迹为二阶点列。由于两个线束所在平面上的任何直线u将把两个线束截成两个射影相关的点列，根据§47与§49，它们最多只有两个自对应点。这样的自对应点显然就是两个射线束的对应的射线的交点。

56. 退化的二阶点列
　　当两个线束为透视相关情况下，轨迹将退化为两条直线，如图56-1所示，其中一条就是透视轴a，另一条为线束的共同射线S1S2，在它上面的任何点都可看作两个线束对应射线的交点。

图56-1 两个线束为透视时二阶点列退化为两条直线

57. 二阶线束
　　类似地，我们可以研究两个射影相关点列对应点的连线系统。我们将两个这样的点列投射到平面的一个点。就得到两个具有共同中心S的射影相关的线束（如前面图47-2那样），其中最多只有两个自对应线。而这样的射线明显就是连接两个点列对应点的直线。可以把结果陈述如下：
　　由两个射影相关的点列对应点的连线构成的射线束，与平面上任何线束最多只有两根射线为共同的射线。因此这样的射线系统称二阶射线束。

58. 退化的二阶线束
　　在两个点列为透视对应的情况下，这一射线系统退化为两个一阶的射线束，如图50-1所示，其中之一是两个点列的共同透视中心S，另一个是两点列的交点M’。任何通过它们的射线可以看两点列对应点的连线。

59. 二阶圆锥面
　　空间的对应定理可以利用平面定理中的点和线连接到空间一点S后方便地得到。平面上具有交点的两个射影线束到空间中就可引出具有相交轴的两个射影面束。对应平面的交线均通过S以及由两个线束生成的二阶点列的点。 它们这样就形成了一个二阶园锥曲面的直线（法线）。所以称它们为二阶圆锥曲面或二次圆锥面（quadric cone），是因为空间每一个不通过S的平面把它切割成为一个二阶点列，并且每条线与它最多切割于两点。
　　如果我们将二个点列投影到一个空间点S，我们就得到两个具有共同中心但在不同平面的射线束。这些线束对应的直线决定了连接两点列对应点到空间点S所投影的平面。这样的平面最多有两个可通过从S出发的所有射线。它就称为二阶平面束。
 

第三章习题
1. 一个人A沿一条笔直的路u向一个方向前进，另一人B在后面沿同一条路向同一个方向前进，并从路边的一个小镜子M上始终看到A。 试问他们有几次会走到一起？他们是始终沿此路的同一个方向的前进的吗？

2. 第一个问题中，当他们沿路走时，两人能从两面镜子M和N中互相看见的机会有几次？ (两个镜子的平面与U.不一定是平行的)

3. 当A沿u移动时，作出B的路程的轨迹，使两人能从两个镜子里始终互相看到。

4. 两名儿童沿两条不同的道路u和u’在走动，并分别拉住一根绳子的两端，使他们二者之间保持一定的距离。已知他们走路的速度不同，但每个人的速度是常数。请问包含绳子的直线将通过道路平面上的任意一点有多少次？

5. 两名儿童以同一速度在两个道路上走动，但不是从两个道路相交的点同时开始。试跟踪绳索所在直线的轨迹。

6. 一艘兵舰在一条笔直的航道上前进，将一门炮瞄准着岸上的一个固定点。试证明，与炮的瞄准方向成直角并通过炮口的直线，或者有两次通过平面上的任何点，或者一次也不通过。 (考虑由通过岸上的点、并与炮的瞄准方向成直角的直线所切割的无穷远点列。)

7. 两条直线u和u’ 在同一平面上分别绕点U和U’旋转。U和U’本身又在同一方向以同一速率移动，但开始时有一个初始夹角。证明它们生成一个二阶点列。

8. 试问在上题中，两条直线什么时候绕相反方向旋转？您能识别它的轨迹吗？

（本章文本上载完）