对支持向量机的求解都是将上节说的原问题转化为对偶问题进行求解的，这些内容都是最优化课程中的内容。
回忆上节的内容，我们的目标是寻找函数在若干约束条件下的最小值。在上节的原问题中，约束条件是包含不等式的，本节先考虑简单的问题，即考虑只包含等式约束的最优化问题：
（1）
其中f(x)被称作目标函数，而下面是一系列的等式约束。回想一下，当没有任何约束存在的时候，应该怎样寻找最优点呢？事实上x*是最优点的必要条件是：
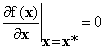
而如果函数f(x)是凸函数的话，这个条件也是充分条件（关于凸函数，请参考维基百科）。
插入一个说明，如果函数f(x)是一个实值函数，x是一个n维向量，那么f(x)对向量x的导数被定义为：
回到目前的问题，当我们寻找约束存在时的最优点的时候，约束的存在虽然减小了需要搜寻的范围，但是却使问题变得更加复杂。为了使问题变得易于处理，我们的方法是把目标函数和约束全部融入一个新的函数，即拉格朗日函数，再通过这个函数来寻找最优点。
为了形象化地分析这个问题，我们考虑目标函数是三变量的函数并且只有一个约束的情况：
（2）
从几何上来看，上面的问题（2）就是从曲面
上来寻找函数
的最小值。假设问题（2）的最优解是
。我们现在做曲面Ω上任一条通过点x的光滑曲线l：
（由于曲线l是在曲面Ω上的，所以自然有
）。
令最优点对应的t为t*。因为x*是曲面Ω上的最优点，所以x*也是曲线l上的最优点，所以t*是一元函数
的最优点，所以在这一点它的导数是0。通过链式法则我们得到：
这个式子说明了在x*这一点，函数的梯度向量
和曲线l在x*处的切线是垂直的。由于曲线l是任意的，所以梯度向量和曲面Ω是垂直的。
回忆高等数学的结论，
的方向就是曲面Ω的法线方向，所以和必然在同一直线的方向上，所以必定存在一个常数μ*，有
。
我们可以把它写成更加精炼的形式。如果我们构造二元函数
，上面的结论就可以表达为必定存在着常数μ*，使
。
我们把构造的函数称作拉格朗日函数，而其中的μ称作拉格朗日乘子。
关于只有等式约束的拉格朗日函数的引入，也可以参考维基百科中的两个变量函数的例子。
以上是一个特殊情形的分析，并且只包含了一个约束。那么包含等式约束的一般情况，也就是问题（1）来说，我们同样可以构造拉格朗日函数，不过由于包括多个等式约束，表达稍微不同：
其中
，
。
也就是说，每一个等式约束都对应着一个拉格朗日乘子。那么x*是最优点的必要条件就是，存在相应的拉格朗日乘子μ*，使得以下两个式子成立：
(3)
(4)
（实际上就是原问题（1）的约束条件换了种写法）
这两个式子就是最优点的必要条件，当然如果函数
是凸函数的话，这两个式子也是充分条件。
现在我们的目标达到了，也就是把目标函数和一系列的等值约束融合到了一个函数（拉格朗日函数）里面，这样只需要解（3）和（4）这两个式子就可以找到最优点，其优点是不言而喻的。而在下一节中我们将会讨论包含不等式约束的最优化问题。