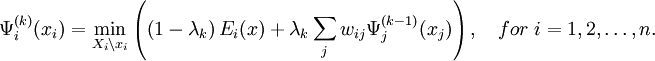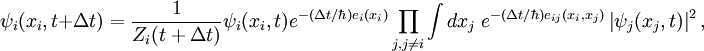最优化:拟牛顿法、最速下降法、共轭梯度法、信赖域法、协同优化
![]() (2012-02-25 18:16:36)
(2012-02-25 18:16:36)
最优化理论与算法是一个重要的数学分支,它所研究的问题是讨论在众多的方案中什么样的方案最优以及怎样找出最优方案。这类问题普遍存在。例如,工程设计中怎样选择设计参数,使得设计方案既满足设计要求又能降低成本;资源分配中,怎样分配有限资源,使得分配方案既能满足各方面的基本要求,又能获得好的经济效益;生产计划安排中,选择怎样的计划方案才能提高产值和利润;原料配比问题中,怎样确定各种成分的比例,才能提高质量,降低成本;城建规划中,怎样安排工厂、机关、学校、商店、医院;住户和其他单位的合理布局;才能方便群众;有利于城市各行各业的发展;农田规划中,怎样安排各种农作物的合理布局,才能保持高产稳产,发挥地区优势;军事指挥中,怎样确定最佳作战方案,才能有效地消灭敌人,保存自己,有利于战争的全风在人类活动的各个领域中,诸如此类,不胜枚举。最优化这一数学分文,正是为这些问题的解决,提供理论基础和求解方法,它是一门应用广泛、实用性强的学科。
20世纪40年代以来,由于生产和科学研究突飞猛进地发展,特别是电子计算机日益广泛应用,使最优化问题的研究不仅成为一种迫切需要,而且有了求解的有力工具。因此最优化理论和算法迅速发展起来,形成一个新的学科。至今已出现线性规划、整数规划、非线性规划、几何规划、动态规划、随机规划、网络流等许多分文。
最优化理论和算法在实际应用中正在发挥越来越大的作用。课程内容:最优化理论与算法包括线性规划单纯形方法、对偶理论、灵敏度分析、运输问题、内点算法、非线性规划K-T条件、无约束最优化方法、约束最优化方法、参数线性规划、运输问题、线性规划路径跟踪法、信赖域方法、二次规划路径跟踪法、整数规划和动态规划等内容。本课程有大量经典的和新近的算法,有比较系统的理论分析,实用性比较强;定理的证明和算法的推导主要以数学分析和线性代数为基础,学习比较容易。
线性和非线性最优化理论、方法、软件及应用
最优化在航空航天、生命科学、水利科学、地球科学、工程技术等自然科学领域和经济金融等社会科学领域有着广泛和重要的应用, 它的研究和发展一直得到广泛的关注. 最优化的研究包含理论、方法和应用.最优化理论主要研究问题解的最优性条件、灵敏度分析、解的存在性和一般复杂性等.而最优化方法研究包括构造新算法、证明解的收敛性、算法的比较和复杂性等.最优化的应用研究则包括算法的实现、算法的程序、软件包及商业化、在实际问题的应用.
这里简介一下线性和非线性最优化理论、方法及应用研究的发展状况.
6
d% u0 g, \# e8 z6 _! t
1. 线性最优化
线性最优化,
又称线性规划, 是运筹学中应用最广泛的一个分支.这是因为自然科学和社会科学中许多问题都可以近似地化成线性规划问题. 线性规划理论和算法的研究及发展共经历了三个高潮, 每个高潮都引起了社会的极大关注. 线性规划研究的第一高潮是著名的单纯形法的研究. 这一方法是Dantzig在1947年提出的,它以成熟的算法理论和完善的算法及软件统治线性规划达三十多年.
随着60年代发展起来的计算复杂性理论的研究, 单纯形法在七十年代末受到了挑战. 1979年前苏联数学家Khachiyan提出了第一个理论上优于单纯形法的所谓多项式时间算法--椭球法,
曾成为轰动一时的新闻, 并掀起了研究线性规划的第二个高潮. 但遗憾的是广泛的数值试验表明, 椭球算法的计算比单纯形方法差.
1984年Karmarkar提出了求解线性规划的另一个多项式时间算法.
这个算法从理论和数值上都优于椭球法, 因而引起学术界的极大关注, 并由此掀起了研究线性规划的第三个高潮. 从那以后, 许多学者致力于改进和完善这一算法,得到了许多改进算法.这些算法运用不同的思想方法均获得通过可行区域内部的迭代点列, 因此统称为解线性规划问题的内点算法. 目前内点算法正以不可抗拒的趋势将超越和替代单纯形法.
线性规划的软件, 特别是由单纯形法所形成的软件比较成熟和完善.这些软件不仅可以解一般线性规划问题, 而且可以解整数线性规划问题、进行灵敏度分析, 同时可以解具有稀疏结构的大规模问题.CPLEX是Bixby基于单纯形法研制的解线性和整数规划的软件, CPLEX的网址是http://www.cplex.com/.
此外,这个软件也可以用来解凸二次规划问题, 且特别适合解大规模问题. PROC LP是SAS软件公司研制的SAS商业软件中OR模块的一个程序.
这个程序是根据两阶段单纯形法研制的,可以用来解线性和整数规划问题并可进行灵敏度分析, 是一个比较完善的程序.用户可以根据需要选择不同的参数来满足不同的要求。关于内点法的软件也在研制之中.BPMPD是Cs.Mzos基于原始对偶内点法研制的解线性和整数规划的软件,其FTP地址是ftp://ftp.sztaki.hu/pub/oplab/SOFTWARE/BPMPD/,可以自由下载.此外,在互联网上能访问到的解线性和整数规划问题的软件还有:EQPS(线性,整数和非线性规划),FMP(线性和混合整数规划),HS/LPLO(线性规划),KORBX(线性规划),LAMPS(线性和整数规划),LPBLP(线性规划),MILP(混合整数规划),MINTO(混合整数规划),
MPSIII(线性和混合整数规划),OML(线性和混合整数规划), OSL(线性,二次和混合整数规划),PROCLP(线性和整数规划),WB(线性和混合整数规划),WHIZARD(线性和混合整数规划),XPRESSMP(线性和混合整数规划)等.
;
y% U! U$ Y. e2 D) E+ Z" n0 `
2.非线性最优化
在实际研究工作和生产实践中存在大量非线性最优化问题, 把它们完全简化成线性问题来处理是不妥当的.随着科学技术和计算机的发展, 这些实际问题具有这样一些特点.一是问题的变量比较多,
因为问题涉及的因素越来越多; 二是问题的规模越来越大;三是问题越来越复杂, 问题的非线性程度越来越高. 这类问题通常描述成在一组非线性约束条件下寻求某一非线性目标函数的最小或最大值。
非线性规划的一个重要理论是1951年Kuhn-Tucker最优条件(简称KT条件)的建立.此后的50年代主要是对梯度法和牛顿法的研究.以Davidon(1959), Fletcher和Powell(1963)提出的DFP方法为起点,
60年代是研究拟牛顿方法活跃时期, 同时对共轭梯度法也有较好的研究. 在1970年由Broyden,Fletcher,Goldfarb 和Shanno从不同的角度共同提出的BFGS方法是目前为止最有效的拟牛顿方法. 由于Broyden, Dennis 和More的工作使得拟牛顿方法的理论变得很完善. 70年代是非线性规划飞速发展时期, 约束变尺度(SQP)方法(Han和Powell为代表)和Lagrange乘子法(代表人物是Powell 和Hestenes)是这一时期主要研究成果.计算机的飞速发展使非线性规划的研究如虎添翼.80年代开始研究信赖域法、稀疏拟牛顿法、大规模问题的方法和并行计算,
90年代研究解非线性规划问题的内点法和有限储存法. 可以毫不夸张的说, 这半个世纪是最优化发展的黄金时期.
与线性规划相比,非线性规划软件还不够完善. 但是已有大量解非线性规划问题的软件, 其中有相当一部分可从互联网上免费下载.BTN是利用线搜索技术的块截断牛顿方法解无约束问题的软件,近似牛顿方向是通过块共轭梯度法解牛顿方程得到. 块状结构比较方便对线性代数方程和函数计算进行并行化处理. BTN有两个版本:
简本和用户版本. 简本不需并行化技术, 而用户版本允许多种复杂运算, 包含并行化处理. 此软件可以通过
ftp://netlib2.cs.utk.edu/opt获得。BQPD是Fletcher研制的解二次规划的软件,
所使用的基本方法是零空间积极集法. DONLP2是Spellucci研制的用SQP方法解一般非线性约束问题的软件,适合解小规模优化问题, 可以从网址ftp://netlib2.cs.utk.edu/opt/donlp2/上免费下载。HOOKE是解无约束最优化问题的一个直接方法的软件,可以通过 ftp: //netlib2.cs.utk.edu /opt /hooke.c获得。LANCELOT是由Conn,Gould和Toint研制的解大规模最优化问题的软件包,适合解无约束最优化、非线性最小二乘、边界约束最优化和一般约束最优化问题.这个软件的基本思想是利用增广Lagrange函数来处理约束条件,
在每步迭代中解一个边界约束优化子问题, 其所用的方法结合信赖域和投影梯度等技术.MINPACK是美国Argonne国家实验室研制的软件包,适合求解非线性方程组和非线性最小二乘问题, 所用的基本方法是阻尼最小二乘法, 此软件可以从网上图书馆获得. PROC NLP是SAS软件公司研制的SAS商业软件中OR模块的一个程序,这个程序适合解无约束最优化、非线性最小二乘、线性约束最优化、二次规划和一般约束最优化问题.TENMIN是Schnabel等研制的解中小规模问题($n<100$)的张量方法软件。在互联网上能访问到的解非线性最优化问题的软件还有:CONOPT(非线性规划),DOT(优化设计工具箱),Excel
and Quattro Pro Solvers(线性,整数和非线性规划),FSQP(非线性规划和极小极大问题),GRG2(非线性规划), LBFGS(有限储存法),LINDO(线性、二次和混合整数规划),LSSOL(最小二乘和二次规划),MINOS(线性和非线性规划),NLPJOB(非线性多目标规划), OPTPACK(约束和无约束最优化),PETS(解非线性方程组和无约束问题的并行算法),QPOPT(线性和二次规划),SQOPT(大规模线性和凸二次规划),SNOPT(大规模线性、二次和非线性规划),SPRNLP(稀疏最小二乘,稀疏和稠密非线性规划),SYSFIT(非线性方程组的参数估计),TENSOLVE(非线性方程组和最小二乘),
VE10(非线性最小二乘)等.
3.最优化的应用
最优化的应用是非常广泛的, 下面仅就最优化在金融和航空方面的应用作一点介绍.
3.1金融和最优化
随着世界经济的发展和知识经济的到来,
金融数学已变成一个热门研究课题,普遍得到各国政府的重视和支持. 而金融数学的一个重要方面是与优化理论及算法相联系的. 诺贝尔经济学奖得主马尔柯维茨提出证券组合选择的均值--方差模型(MV模型)便是一个二次规划问题. 这个模型使得证券组合选择方法实现了从定性描述到定量描述质的飞跃,使得人们可以科学而准确地分析与选择投资策略.s4
a2 Z% [5 F M; Y% ?* `5 V
3.2 航空和最优化
最优化在航空方面的应用也很多.从90年代引起国际学术界重视的"气动数值优化设计"是计算流体力学和优化设计技术相结合来研究飞行器气动性能及其它流动问题的方法. 这一方法的研究包含了大量的最优化算法和应用研究.
在航空航天广泛应用的结构优化设计是最近三十多年来发展起来的一门新兴的现代化科学技术. 它的发展是与最优化理论和方法的发展是密不可分的. 从60年代起, 结构设计问题开始用一般非线性规划问题来处理. 此后, 一种新的优化理论和方法一出现并被用到结构设计问题上来, 从而推动了结构优化设计的快速发展.目前处于优化研究热点的信赖域法被用于解飞机设计中颤振问题模型,
收到了良好效果.
最优化
最优化,是应用数学的一个分支,主要研究以下形式的问题:
-
给定一个函数
 ,寻找一个元素
,寻找一个元素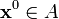 使得对于所有A中的
使得对于所有A中的 ,
, (最小化);或者
(最小化);或者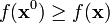 (最大化)。
(最大化)。
这类定式有时还称为“数学规划”(譬如,线性规划)。许多现实和理论问题都可以建模成这样的一般性框架。
典型的,A一般为欧几里得空间 中的子集,通常由一个A必须满足的约束等式或者不等式来规定。 A的元素被称为是可行解。函数f被称为目标函数,或者费用函数。一个最小化(或者最大化)目标函数的可行解被称为最优解。
中的子集,通常由一个A必须满足的约束等式或者不等式来规定。 A的元素被称为是可行解。函数f被称为目标函数,或者费用函数。一个最小化(或者最大化)目标函数的可行解被称为最优解。
一般情况下,会存在若干个局部的极小值或者极大值。局部极小值x * 定义为对于一些δ
> 0,以及所有的x 满足
-
 ;
;
公式
成立。这就是说,在 周围的一些闭球上,所有的函数值都大于或者等于在该点的函数值。一般的,求局部极小值是容易的,但是要确保其为全域性的最小值,则需要一些附加性的条件,例如,该函数必须是凸函数。
周围的一些闭球上,所有的函数值都大于或者等于在该点的函数值。一般的,求局部极小值是容易的,但是要确保其为全域性的最小值,则需要一些附加性的条件,例如,该函数必须是凸函数。
符号表示
最优化问题通常有一些较特别的符号标示方法。例如:
这是要求表达式x2 + 1的最小值,这里x取值为全体实数,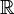 。这个问题的最小值应该是1,当x =
。这个问题的最小值应该是1,当x =
0。
这是要求表达式2x的最大值,同样地,x在全体实数上取值。对于这个问题,由于该表达式不是有上界的,因此不存在最大值,因此,答案应该是无限大,或者是不可定义的。
这是求使表达式x2+1 达到最小值时x的值。在这里x被限定在区间[-∞ ,-1]之间,所以上式的值是-1。
主要分支
- 线性规划
- 当目标函数f是线性函数而且集合A是由线性等式函数和线性不等式函数来确定的, 我们称这一类问题为线性规划
- 整数规划
- 当线性规划问题的部分或所有的变量局限于整数值时,我们称这一类问题为整数规划问题
- 二次规划
- 目标函数是二次函数,而且集合A必须是由线性等式函数和线性不等式函数来确定的。
- 非线性规划
- 研究的是目标函数或是限制函数中含有非线性函数的问题。
- 随机规划
- 研究的是某些变量是随机变量的问题。
- 动态规划
- 研究的是最优策略基于将问题分解成若干个较小的子问题的优化问题。
- 组合最优化
- 研究的是可行解是离散或是可转化为离散的问题。
- 无限维最优化
- 研究的是可行解的集合是无限维空间的子集的问题,一个无限维空间的例子是函数空间。
手法
对于无约束的优化问题, 如果函数是二次可微的话,可以通过找到目标函数梯度为0(也就是鞍点)的那些点来解决此优化问题。我们需要用黑塞矩阵来确定此点的类型。如果黑塞矩阵是正定的话,该点是一个局部最小解,如果是负定的话,该点是一个局部最大解,如果黑塞矩阵是不定的话,该点是某种鞍点。
要找到那些拐点,我们可以通过猜测一个初始点,然后用比如以下的迭代的方法来找到。
如果目标函数在我们所关心的区域中是凸函数的话,那么任何局部最小解也是全局最优解。现在已经有稳定,快速的数值计算方法来求二次可微地凸函数的最小值。
有约束条件的约束问题常常可以通过拉格朗日乘数转化为非约束问题。
其他一些流行的方法有:
人工智能和最优化
现代的计算机科学技术和人工智能科学把最优化作为一个重要的领域来研究。我们也可以认为人工智能的一些算法,就是模拟了人类寻求实际问题最优解的过程。例如,利用人工智能方法设计软件,配合外部的电子设备例如摄像头识别人脸;利用数据采矿和神经网络算法来寻找投资的最佳时机等等。
参见
参考
-
Stephen Boyd and Lieven Vandenberghe (2004). Convex
Optimization,Cambridge University Press. ISBN
0-521-83378-7.
外部链接
最优化牛顿法
这是一套最优化课件,包括:牛顿法、线性规划、梯度法、共轭梯度法、搜索法、单纯形调优法、单纯形替换法、对偶单纯形、约束优化、无约束最优化、一维最优化。
拟牛顿法
概述
拟牛顿法(Quasi-Newton Methods)是求解非线性优化问题最有效的方法之一,于20世纪50年代由美国Argonne国家实验室的物理学家W. C. Davidon所提出来。Davidon设计的这种算法在当时看来是非线性优化领域最具创造性的发明之一。不久R. Fletcher和M.
J. D. Powell证实了这种新的算法远比其他方法快速和可靠,使得非线性优化这门学科在一夜之间突飞猛进。在之后的20年里,拟牛顿方法得到了蓬勃发展,出现了大量的变形公式以及数以百计的相关论文。 拟牛顿法和最速下降法(Steepest Descent Methods)一样只要求每一步迭代时知道目标函数的梯度。通过测量梯度的变化,构造一个目标函数的模型使之足以产生超线性收敛性。这类方法大大优于最速下降法,尤其对于困难的问题。另外,因为拟牛顿法不需要二阶导数的信息,所以有时比牛顿法(Newton's Method)更为有效。如今,优化软件中包含了大量的拟牛顿算法用来解决无约束,约束,和大规模的优化问题。 拟牛顿法的基本思想如下。首先构造目标函数在当前迭代$x_k$的二次模型:m_k(p)=f_k+g_k^T
p+p^T B_k p/2,这里f_k=f(x_k),g_k=▽f(x_k),B_k是一个对称正定矩阵。于是我们取这个二次模型的最优解p_k=-B_k^{-1} g_k作为搜索方向,并且得到新的迭代点x_{k+1}=x_k+a_k p_k,其中我们要求步长a_k满足Wolfe条件。这样的迭代类似与牛顿法,区别就在于用近似的Hesse矩阵B_k代替真实的Hesse矩阵。所以拟牛顿法最关键的地方就是每一步迭代中矩阵B_k的更新。现在假设得到一个新的迭代x_{k+1},并得到一个新的二次模型:m_{k+1}(p)=f_{k+1}+g_{k+1}^T
p + p^T B_{k+1} p/2。我们尽可能地利用上一步的信息来选取B_{k+1}。具体地,我们要求g_{k+1}-g_k=a_k B_{k+1} p_k,从而得到B_{k+1}s_k=y_k,其中s_k=x_{k+1}-x_k,y_k=g_{k+1}-g_k。这个公式被称为割线方程。下面主要介绍这几种方法:DFP方法,BFGS方法,SR1方法,Broyden族方法。
DFP方法
记H_k=B_k^{-1},DFP公式为H_{k+1}=H_k-(H_ky_ky_k^TH_k)/(y_k^T H_k y_k)+(s_ks_k^T)/(y_k^Ts_k)。该公式最初由Davidon于1959年提出,随后被Fletcher和Powell研究和推广。DFP方法是秩-2更新的一种,由它产生的矩阵B_k是正定的,而且满足这样的极小性:min
||B-B_k|| s.t. B=B^T, Bs_k=y_k。
BFGS方法
DFP更新公式非常有效,但很快就被BFGS公式取代。BFGS与DFP十分类似,是另一种秩-2更新,以其发明者Boyden, Fletcher, Goldfarb和Shanno的姓氏首字母命名。BFGS公式为B_{k+1}=B_k-(B_ks_ks_k^TB_k)/(s_k^T B_k s_k)+(y_ky_k^T)/(y_k^Ts_k)。由他产生的矩阵B_k同样保持正定性,而且也满足一个极小性:min
||H-H_k|| s.t. H=H^T, Hy_k=s_k。BFGS和DFP公式在形式上是对称的:B_k与H_k对称,s_k与y_k对称。但是BFGS比DFP更加有效。
SR1方法
有别于DFP和BFG方法,SR1是一种秩-1更新。它的公式是:B_{k+1}=(y_k-B_ks_k)(y_k-B_ks_k)^T/((y_k-B_ks_k)^Ts_k)。SR1公式不要求矩阵B_k保持正定性,从而更逼近真实的Hesse矩阵,所以适用于信赖域方法(Trust Region
Methods)。
Broyden族
Boyden族是更广泛的一类更新公式,其形式为:B_{k+1}=(1-c_k)B_{k+1}^{BFGS}+c_k B_{k+1}^{DFP}。当c_k=0时,Broyden族公式就变成了BFGS公式;当c_k=1时,Broyden族公式就变成了DFP公式。因此BFGS和DFP均可看成Broyden族的特殊形式或者其中一员。
拟牛顿法/Quasi-Newton,DFP算法/Davidon-Fletcher-Powell,及BFGS算法/Broyden-Fletcher-Goldfarb-Shanno
什么?牛顿法是什么?本文是基于你已经知道牛顿法的原理的假设,如果你不清楚,那么可以看我这篇文章,里面非常简单而又清晰地描述了牛顿法的原理。
了解了牛顿法的原理,我们就知道了:在每一次要得到新的搜索方向的时候,都需要计算Hesse矩阵(二阶导数矩阵)。在自变量维数非常大的时候,这个计算工作是非常耗时的,因此,拟牛顿法的诞生就有意义了:它采用了一定的方法来构造与Hesse矩阵相似的正定矩阵,而这个构造方法计算量比牛顿法小。这就是对它”有什么用“的回答了。
(1)DFP算法
下面,就从DFP算法来看看“拟牛顿”是如何实现的(DFP算法是以Davidon、Fletcher、Powell三位牛人的名字的首字母命名的)。
前面说了,Hesse矩阵在拟牛顿法中是不计算的,拟牛顿法是构造与Hesse矩阵相似的正定矩阵,这个构造方法,使用了目标函数的梯度(一阶导数)信息和两个点的“位移”(Xk-Xk-1)来实现。有人会说,是不是用Hesse矩阵的近似矩阵来代替Hesse矩阵,会导致求解效果变差呢?事实上,效果反而通常会变好。有人又会问为什么?那么就简要地说一下——
由牛顿法的原理可知如下几个等式:
若最后一个等式子的最左边
< 0,即,就是直观概念上的“沿方向d上,目标函数值下降”的表达。而在逐步寻找最优解的过程中,我们是要求目标函数值下降的,因此,应该有-(X-Xi)A(X-Xi)
< 0,也即
由于涉及到Hesse矩阵(二阶导数矩阵),我们当然要从目标函数
f(X) 的泰勒展开式说开去。与最优化理论中的很多问题一样,在这里,我们依然要假设目标函数可以用二次函数进行近似(实际上很多函数都可以用二次函数很好地近似):
忽略高阶无穷小部分,只看前面的3项,其中A为目标函数的Hesse矩阵(二阶导数矩阵)。此式两边对X求导得:
于是,当
X=Xi 时,将[2]式两边均左乘(Ai+1)-1,有:
上式左右两边近似相等,但如果我们把它换成等号,并且用另一个矩阵H来代替上式中的A-1,则得到:
这个方程,就是拟牛顿方程,其中的矩阵H,就是Hesse矩阵的逆矩阵的一个近似矩阵。但是,从初始的H0开始,如何得到每一步迭代过程中需要的H1,H2,……呢?在迭代过程中生成的矩阵序列H0,H1,H2,……中,每一个矩阵Hi+1,都是由前一个矩阵Hi修正得到的,这个修正方法有很多种,这里只说DFP算法的修正方法。设:
然后又有问题:矩阵E怎么求?再设:
其中,m和n均为实数,v和w均为N维向量。将[6]代入[5]式,再将[5]式代入[4]式,可得:
[8]式与[7]式完全相同,只不过用简化的记号重写了一下。如果求出了m,n,v,w,就可以知道[6]式怎么求,从而进一步知道[5]式怎么求,从而我们的问题就彻底解决了。符合[7]这个方程的v,w可能有很多,但是我们有没有可能找到v,w的一个“特例”,使之符合这个等式呢?仔细观察一下,是可以找到的:[7]式的右边两个向量相减的结果,是一个n×1的向量,因此,等式左边的计算结果当然也是一个n×1的向量(每一项都是一个n×1的向量),所以我们把[7]式写成了[8]式的样子,可以看到,其中的第二、第三项中的括号里的向量的点积均为实数,这里,可以使第一个括号中的mvTqi值为1,使第二个括号中的nwTqi值为-1,这样的话,v只要取si,w只要取Hiqi,就可以使[8]式成立了。的确,这种带有一点猜测性质的做法,确实可以让我们找到一组适合的m,n,v,w值。
所以,我们得到的m,n,v,w值如下:
现在我们几乎大功告成了:将[8]~[11]代入[6]式,然后再将[6]代入[5]式,就得到了Hesse矩阵的逆矩阵的近似阵H的计算方法:
在上面的推导过程中,有人可能觉得有点无厘头:为什么[6]式要那样假设,是怎么想到的?我能给出的答案是:这一点我也没想明白。如果你知道,请告诉我,非常感谢。某些书上经常写类似于“很显然,XXX”之类的话,从一个定理直接得出了一个让人摸不着头脑的结论,而作为我这样比较笨的人来说,我觉得写书的很多专家们认为“很显然”的东西一点也不“显然”,甚至于有时候,我觉得那就像凤姐突然变成了范冰冰一样——一下子变出来了一个漂亮的结论,难以相信。所以这也是为什么我花费了很多时间,来把一些“很显然”的东西记下来,写明白的原因了。对于大多数牛人,他们需要的当然不是这种思维跨度这么小的文章,而是那种从地球可以一下子飞到火星的文章。所以,我写的东西不适合于水平高的人看,我只期望能帮助一小部分人就知足了。
说到这里,那么到底什么是DFP算法呢?上面的矩阵H的计算方法就是其核心,下面再用简单的几句话描述一下DFP算法的流程:
已知初始正定矩阵H0,从一个初始点开始(迭代),用式子
有人会说,上面那些乱七八糟的都是搞什么啊,猜来猜去的就折腾出了一个公式,然后就确定这公式能用了?就不怕它在迭代的时候根本无法寻找到目标函数的极小值?正因为有这些疑问,所以在这里,还要提及一个非常重要的问题:我们通过带有猜测性质的做法,得到了矩阵H的计算公式,但是,这个修正过的矩阵,能否保持正定呢?前面已经说了,矩阵H正定是使目标函数值下降的条件,所以,它保持正定性很重要。可以证明,矩阵H保持正定的充分必要条件是:
并且,在迭代过程中,这个条件也是容易满足的。此结论的证明并不复杂,但是为了不影响本文的主旨,这里就没有必要写出来了。总之,我觉得作为一个最优化的学习者来说,首先要关注的是不是这些细节问题,而是先假设这些算法都适用,然后等积累到一定程度了,再去想“为什么能适用”的问题。
(2)BFGS算法
在上面的DFP算法的推导中,我们得到了矩阵H的计算公式,而BFGS算法和它有点像,但是比它形式上复杂一点。尽管它更复杂,但是在BFGS算法被Broyden,Fletcher,Goldfarb,Shanno四位牛人发明出来到现在的40多年时间里,它仍然被认为是最好的拟牛顿算法。历史总是这样,越往后推移,人们要超越某种技术所需的时间通常就越长。但是我们很幸运地可以站在巨人的肩膀上,从而可以在使用前人已经发明的东西的基础上感叹一声:这玩意太牛了。
好吧,又扯远了……
回到中心主题,看看在BFGS算法中,与上面的[13]式一样的矩阵H是如何计算的:
在[14]式中,最后一项(深蓝色的部分)就是BFGS比DFP多出来的东西。其中,w为一个n×1的向量。我们看到,由于向量w的表达式太长,所以没有把它直接写在[14]式中,而是单独列在了[15]式里。
可能[14]式一看就让人头晕,所以先来弱弱地解释一下这个式子的计算结果(如果你觉得好雷人,那么请直接无视):wwT是一个n×1的向量与一个1×n的向量相乘,结果为一个n×n的矩阵,而[14]式中最后一项里,除了wwT之外的那一部分是(1×n)向量、n×n矩阵、n×1向量相乘,结果为一实数,因此[14]式最后一项结果为一个n×n矩阵,这与[14]式等号左边的矩阵H为n×n矩阵一致。这一点没有问题了。
在目标函数为二次型(“在数学中,二次型是一些变量上的二次齐次多项式”)时,无论是DFP还是BFGS——也就是说,无论[14]式中有没有最后一项——它们均可以使矩阵H在n步之内收敛于A-1。
延伸阅读:BFGS有一个变种(我不知道这样称呼是否正确),叫作“Limited-memory
BFGS”,简称“L-BFGS”或“LM-BFGS”(这里的“LM”与Levenberg-Marquard算法没有关系),从它的名字上看,你肯定能猜到,使用L-BFGS算法来编写程序时,它会比BFGS算法占用的内存小。从前面的文章中,我们知道,BFGS在计算过程中要存储一个n×n的矩阵,当维数n很大的时候,这个内存占用量会很大——例如,在10万维的情况下,假设矩阵H中的元素以double来存储,那么,内存占用即为100000×100000×8÷1024÷1024÷1024≈74.5(GB),这太惊人了,一般的服务器几乎无法承受。所以,使用L-BFGS来降低内存使用量在某些情况下是非常有意义的。
关于L-BFGS的英文解释,请点击这个Wiki链接。由于我还没有深入学习L-BFGS,所以没办法在这里详细叙述了。
http://www.codelast.com/?p=2780
最速下降法
f (x)的一种重要解析法,研究最速下降法原理及其算法实现对我们有着极其重要的意义。
最速下降法
1.最速下降方向
函数f(x)在点x处沿方向d的变化率可用方向导数来表示。对于可微函数,方向导数等于梯度与方向的内积,即:
Df(x;d)
因此,求函数f(x)在点x处的下降最快的方向,可归结为求解下列非线性规划:
min
s.t.
当
时等号成立。因此,在点x处沿上式所定义的方向变化率最小,即负梯度方向为最速下降方向。
2.最速下降算法
最速下降法的迭代公式是
x(k+1)
其中d(k)是从x(k)出发的搜索方向,这里取在x(k)处的最速下降方向,即
d
λk是从x(k)出发沿方向d(k)进行一维搜索的步长,即λk满足
f(x(k)
计算步骤如下:
(1)给定初点x(1)
(2)计算搜索方向d
(3)若||d(k)||
f(x(k)
(4)令x(k+1)
http://www.cnblogs.com/yangxi/archive/2011/10/20/2219408.html
描述
梯度下降法,基于这样的观察:如果实值函数 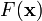 在点
在点 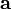 处可微且有定义,那么函数
处可微且有定义,那么函数 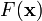 在
在 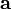 点沿着梯度相反的方向
点沿着梯度相反的方向  下降最快。
下降最快。
因而,如果
对于 γ
> 0 为一个够小数值时成立,那么 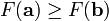 。
。
考虑到这一点,我们可以从函数 F 的局部极小值的初始估计  出发,并考虑如下序列
出发,并考虑如下序列 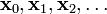 使得
使得
因此可得到
如果顺利的话序列 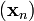 收敛到期望的极值。注意每次迭代步长 γ 可以改变。
收敛到期望的极值。注意每次迭代步长 γ 可以改变。
右侧的图片示例了这一过程,这里假设 F 定义在平面上,并且函数图像是一个碗形。蓝色的曲线是等高线(水平集),即函数 F 为常数的集合构成的曲线。红色的箭头指向该点梯度的反方向。(一点处的梯度方向与通过该点的等高线垂直)。沿着梯度下降方向,将最终到达碗底,即函数 F值最小的点。
例子
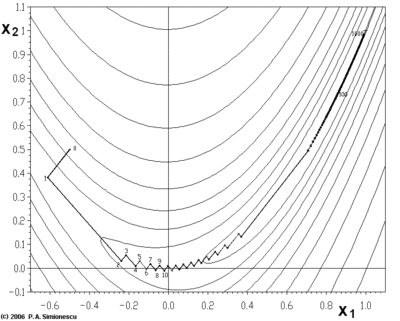
梯度下降法处理一些复杂的非线性函数会出现问题,例如Rosenbrock函数
其最小值在 (x,y)
= (1,1) 处,数值为f(x,y) = 0。但是此函数具有狭窄弯曲的山谷,最小值(x,y)
= (1,1) 就在这些山谷之中,并且谷底很平。优化过程是之字形的向极小值点靠近,速度非常缓慢。
下面这个例子也鲜明的示例了"之字"的下降,这个例子用梯度下降法求  的极小值。
的极小值。
缺点
由上面的两个例子,梯度下降法的缺点是 [1]:
- 靠近极小值时速度减慢。
- 直线搜索可能会产生一些问题。
- 可能会'之字型'地下降。
参阅
参考文献
-
Mordecai Avriel (2003). Nonlinear Programming: Analysis and Methods. Dover Publishing. ISBN
0-486-43227-0. -
Jan A. Snyman (2005). Practical Mathematical Optimization: An Introduction to Basic Optimization Theory and Classical and New Gradient-Based
Algorithms.Springer Publishing. ISBN
0-387-24348-8
共轭梯度法
数学上,共轭梯度法是求解特定线性系统的数值解的方法,其中那些矩阵为对称和正定。共轭梯度法是一个迭代方法,所以它适用于稀疏矩阵系统,因为这些系统对于象乔莱斯基分解这样的直接方法太大了。这种系统在数值求解偏微分方程时相当常见。
共轭梯度法也可以用于求解无约束的最优化问题。
双共轭梯度法提供了一种处理非对称矩阵情况的推广。
|
|
方法的表述
设我们要求解下列线性系统
- Ax = b,,
其中n-×-n矩阵A是对称的(也即,AT = A),正定的(也即,xTAx >
0对于所有非0向量x属于Rn),并且是实系数的。
将系统的唯一解记作x*。
最后算法
经过一些简化,可以得到下列求解Ax = b的算法,其中A是实对称正定矩阵。
-
x0
:= 0 -
k
:= 0 -
r0
:= b -
repeat until rk is "sufficiently
small":-
k
:= k + 1 -
if k = 1
-
p1
:= r0
-
p1
-
else
-
- end if
-

-
xk
:= xk-1 +
αk pk -
rk
:= rk-1 -
αk A pk
-
k
- end repeat
- 结果为xk
外部连接
-
Méthode du gradient conjugé(共轭梯度法,法语)作者N.
Soualem. -
Méthode du gradient conjugé préconditionné(预处理共轭梯度法,法语)作者N.
Soualem. -
共轭梯度法通俗介绍作者Jonathan
Richard Shewchuk.
参考
共轭梯度法最初出现于
-
Magnus R. Hestenes and Eduard Stiefel(1952),Methods of conjugate gradients for solving linear systems, J. Research Nat. Bur. Standards 49,
409–436.
下列教科书中可以找到该方法的描述
-
Kendell A. Atkinson(1988),An introduction to numerical analysis(2nd ed.),Section 8.9, John Wiley and Sons. ISBN
0-471-50023-2. -
Gene H. Golub and Charles F. Van Loan, Matrix computations(3rd ed.),Chapter 10, Johns Hopkins University Press. ISBN
0-8018-5414-8.
共轭梯度法
1.共轭方向
无约束问题最优化方法的核心问题是选择搜索方向。
以正定二次函数为例,来观察两个方向关于矩阵A共轭的几何意义。
设有二次函数:
f(x)
其中A是n×n对称正定矩阵,x*是一个定点,函数f(x)的等值面
1/2
是以x*为中心的椭球面,由于
▽f(x*)
A正定,因此x*是f(x)的极小点。
设x(1)是在某个等值面上的一点,该等值面在点x(1)处的法向量
▽f(x(1))
又设d(1)是这个等值面在d(1)处的一个切向量。记作
d(2)
自然,d(1)与▽f(x(1))正交,即d(1)T▽f(x(1))
d(1)TAd(2)
即等值面上一点处的切向量与由这一点指向极小点的向量关于A共轭。

由此可知,极小化式所定义的二次函数,若依次沿着d(1)和d(2)进行一维搜索,则经两次迭代必达到极小点。
1.共轭梯度法
共轭梯度法最初由Hesteness和Stiefel于1952年为求解线性方程组而提出的。后来,人们把这种方法用于求解无约束最优化问题,使之成为一种重要的最优化方法。
Fletcher-Reeves共轭梯度法,简称FR法。
共轭梯度法的基本思想是把共轭性与最速下降方法相结合,利用已知点处的梯度构造一组共轭方向,并沿这组方向进行搜素,求出目标函数的极小点。根据共轭方向基本性质,这种方法具有二次终止性。
对于二次凸函数的共轭梯度法:
min
其中x∈
具体求解方法如下:
首先,任意给定一个初始点x(1),计算出目标函数f(x)在这点的梯度,若||g1||
d(1)
沿方向d(1)搜索,得到点x(2)。计算在x(2)处的梯度,若||g2||
一般地,若已知点x(k)和搜索方向d(k),则从x(k)出发,沿d(k)进行搜索,得到
x(k+1)
其中步长λk满足
f(x(k)
此时可求出λk的显示表达

计算f(x)在x(k+1)处的梯度。若||gk+1||
d(k+1)
上式两端左乘d(k)TA,并令
d(k)TAd(k+1)
由此得到
βk
再从x(k+1)出发,沿方向d(k+1)搜索。
在FR法中,初始搜索方向必须取最速下降方向,这一点决不可忽视。因子βk可以简化为:βk
3.非线性共轭梯度
当目标函数是高于二次的连续函数(即目标函数的梯度存在)时,其对应的解方程是非线性方程,非线性问题的目标函数可能存在局部极值,并且破坏了二次截止性,共轭梯度法需要在两个方面加以改进后,仍然可以用于实际的反演计算,但共轭梯度法不能确保收敛到全局极值。
(1)首先是共轭梯度法不能在n维空间内依靠n步搜索到达极值点,需要重启共轭梯度法,继续迭代,以完成搜索极值点的工作。
(2)在目标函数复杂,在计算时,由于需要局部线性化,需计算Hessian矩阵A,且计算工作量比较大,矩阵A也有可能是病态的。Fletcher和Reeves的方案最为常用,抛弃了矩阵A的计算,具体形式如下:

式中gk-1和gk分别为第k-1和第k次搜索是计算出来的目标函数的梯度。
http://www.cnblogs.com/yangxi/archive/2011/10/20/2219408.html
信赖域法
信赖域算法是求解非线性优化问题的一种数值方法,收敛性较好。该算法在每次迭代时强制性地要求新的迭代点与当前的迭代点之间的距离不超过某一控制量.
引入控制步长是因为传统的线搜索方法常常由于步长过大而导致算法失败,特别是当问题是病态时. 控制步长实质上等价于在以当前迭代点为中心的一个邻域内对一个近似于原问题的简单模型求极值. 这种技巧可理解为只在一个邻域内对近似模型信赖,所以此邻域被称为信赖域(trust region) .MATLAB里有信赖域算法,在优化工具箱里。信赖域算法相关文献很多,估计程序代码也能有。
置信域方法(Trust-region methods)又称为信赖域方法,它是一种最优化方法,能够保证最优化方法总体收敛。
算法发展
置信域方法的历史可以追溯到Levenberg(1944),Marquardt(1963),Goldfeld,Quandt and Trotter(1966),但现代置信域方法是Powell(1970)提出来的。他明确提出了置信域子问题,接受方向步sk的准则,校正置信域半径 的准则,及收敛性定理。这些措施使置信域方法比线性搜索方法具有更大的优越性。
的准则,及收敛性定理。这些措施使置信域方法比线性搜索方法具有更大的优越性。
思想框架
考虑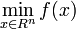 ,其中ƒ(x)是定义在Rn上的二阶连续可微函数。定义当前点的邻域Ωk
,其中ƒ(x)是定义在Rn上的二阶连续可微函数。定义当前点的邻域Ωk
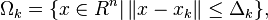
这里Δk称为置信域半径。假定在这个邻域中,二次模型是目标函数ƒ(x)的一个合适的近似,则在这个邻域(称为置信域)中极小化二次模型,得到近似极小点sk,并取,其中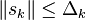 。
。
置信域方法的模型子问题是

其中,s = x − xk,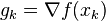 ,Bk是一个对称矩阵,它是黑塞矩阵
,Bk是一个对称矩阵,它是黑塞矩阵 或其近似,Δk>
或其近似,Δk>
0为置信域半径,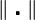 为某一范数,通常我们采用l2范数。
为某一范数,通常我们采用l2范数。
选择Δk的方法:根据模型函数q(k)(s)对目标函数ƒ(x)的拟合程度来调整置信域半径Δk。对于置信域方法的模型子问题的解sk,设目标函数的下降量
Aredk = f(xk)
− f(xk + sk)
为实际下降量,设模型函数的下降量
Predk = q(k)(0)
− q(k)(sk)
为预测下降量。 定义比值
 ,
,
它用来衡量模型函数q(k)与目标函数ƒ
置信域算法
-
步1. 给出初始点x0 ,置信域半径的上界
 ,
, ,
, ,
, ,0
,0
< γ1 < 1 < γ2,
-
步2. 如果
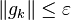 ,停止
,停止 - 步3. (近似地)求解置信域方法的模型子问题,得到 sk
- 步4. 计算ƒ(xk+sk) 和 rk。令

- 步5. 校正置信域半径,令
![最优化:拟牛顿法、最速下降法、共轭梯度法、信赖域法、协同优化 \begin{align}
& {{\Delta }_{k+1}}\in (0,{{\gamma }_{1}}{{\Delta }_{k}}],\quad \quad \quad \quad \ \ \ \text{if }{{r}_{k}}<{{\eta }_{1}}; \\
& {{\Delta }_{k+1}}\in [{{\gamma }_{1}}{{\Delta }_{k}},{{\Delta }_{k}}],\quad \quad \quad \quad \ \text{if }{{r}_{k}}\in [{{\eta }_{1}},{{\eta }_{2}}); \\
& {{\Delta }_{k+1}}\in [{{\Delta }_{k}},\min \{{{\gamma }_{2}}{{\Delta }_{k}},\bar{\Delta }\}],\ \text{if }{{r}_{k}}\ge {{\eta }_{2}}. \\
\end{align}](http://upload.wikimedia.org/wikipedia/zh/math/f/3/d/f3d4d16aeed694f783bb0cbe72853c28.png)
- 步6. 产生Bk+1,校正q(k) ,令k:=k+1 ,转步2。
应用
现今,置信域算法广泛应用于应用数学、物理、化学、工程学、计算机科学、生物学与医学等学科。相信在不远将来,信赖域方法会在更广泛多样的领域有着更深远的的发展。
参考文献
-
Andrew R. Conn,Nicholas I. M. Gould,Philippe L. Toint."Trust-region methods".Philadelphia, Pa.
: SIAM [u.a.], 2000. ISBN
978-0-898714-60-9
信赖域方法及其应用
朱德通
上海师范大学数学系教授
朱教授首先介绍了何为信赖域策略。信赖域策略是目前求解无约束最优化问题min f(x)的一种有效的方法。简单来说信赖域策略的基本思想是:给定一个初始点x0,按照某一迭代格式产生一个点列{xk},希望某一xk是最优化问题的解或点列收敛于解。目前常用的是采用线搜索的技术结合精确线搜索准则(或者其他不精确的线搜索准则,如Wolfe准则、Armijo-Goldstein准则、强Wolfe准则以及回代技术等),在给出下降方向dk后,得到点列{xk}。对于收敛域策略,朱教授还讨论了方法收敛性和评价准则。
基于高斯函数和信赖域更新策略的Kriging响应面法
王成恩1,2,黄章俊1,2,3+
1.东北大学辽宁省复杂装备多学科设计优化技术重点实验室,辽宁沈阳110004;2.东北大学流程工业综合自动化教育部重点实验室,辽宁沈阳110004;3.长沙理工大学能源与动力工程学院,湖南长沙410114
摘要:为建立拟合效率高且能够满足工程精度要求的响应面近似模型,在分析已有响应面建模方法基本特性的基础上,提出一种基于高斯函数和信赖域更新策略的Kriging响应面法。该方法将高斯函数作为设计点之间的相关函数,并在优化过程中采用信赖域更新策略对试验设计的取样区域进行动态修正。通过在四个典型数值算例和某涡轮盘的热—结构优化设计中的应用,验证了所提方法的有效性。
关键词:高斯函数;信赖域更新;多学科设计优化;响应面法;Kriging模型;涡轮盘
中图分类号:TP391.7
参考文献
[1]WANG G G, SHAN S. Review of metamodeling techniques in support of engineering design optimization[J]. Journal of Mechanical Design,2007,129(2):370-380.
[2]FORRESTER A I J, KEANE A J. Recent advances in surrogate-based optimization[J]. Progress in Aerospace Sciences,2009,45(1/2/3):50-79.
袁亚湘在非线性优化计算方法及其理论方面,取得了一系列的重要成果。他的贡献主要集中在信赖域法,拟牛顿法和共轭梯度法三个方面。在信赖域法算法设计和收敛性分析方面所做的工作是开创性的,特别是对于非光滑优化信赖域方法的研究得出了一系列重要的收敛性定理,给出了超线性收敛的充分必要条件。在拟牛顿方法的理论研究方面,袁亚湘和美国科学家合作证明了一类拟牛顿方法的全局收敛性,这是非线性规划算法理论在80年代最重要的成果之一。袁亚湘和学生戴?虹合作提出的“戴—袁方法”被认为是非线性共轭梯度法四个主要方法之一。袁亚湘还首创性地提出了用信赖域方法和传统的线搜索方法的结合来构造新的计算方法,开创了利用非二次模型信息构造二次模型子问题的方法,提出了非拟牛顿方法。国外同行称袁亚湘在信赖域方法领域取得的成就是基石性的成果,他的贡献对最优化领域是至关重要的。
袁亚湘的专业:计算数学、应用数学、运筹学。研究方向:最优化计算方法。
他在非线性优化计算方法及其理论方面,取得了一系列的重要成果,在非线性规划方面的研究成果被国际上命名为“袁氏引理”。他的贡献主要集中在信赖域法,拟牛顿法和共轭梯度法三个方面。在信赖域法算法设计和收敛性分析方面所做的工作是开创性的,特别是对于非光滑优化信赖域方法的研究得出了一系列重要的收敛性定理,给出了超线性收敛的充分必要条件。他因此在1984年获英国剑桥大学数学学部研究生论文竞赛唯一的一等奖,以及1985年在英国伦敦获首届青年国际数值分析奖二等奖。他给出了双球信赖域子问题的最优性条件,证明了截断共轭梯度法的“1/2
猜想”。在拟牛顿方法的理论研究方面,他和美国科学家合作证明了一类拟牛顿方法的全局收敛性,这是非线性规划算法理论在80年代最重要的成果之一。他和学生戴彧虹合作提出的“戴--袁方法”被认为是非线性共轭梯度法四个主要方法之一。他还首创性地提出了用信赖域方法和传统的线搜索方法的结合来构造新的计算方法,开创了利用非二次模型信息构造二次模型子问题的方法,提出了非拟牛顿方法。国外同行称袁亚湘在信赖域方法领域取得的成就是基石性的成果,他的贡献对最优化领域是至关重要的。
信赖域方法http://wenku.baidu.com/view/2a977d294b73f242336c5fee
信赖域方法http://www.docin.com/p-87163751.html
计算数学http://blog.sina.com.cn/s/blog_4b700c4c0102du69.html
组合优化
组合最优化,二维的例子,比如服装厂做衣服,衣服分成很多块,这些块需要从布料上切下来。怎么切,剩下的废布料最少?三维的例子,如集装优化。
组合优化的难处,主要是加进来拓扑分析,不同的拓扑形态下,不同部分的约束关系便不同,算法也就要调整。如果给定一个拓扑形态,组合优化往往就退化成一个整数优化的问题了。
组合最优化
协同优化算法的原理是将一复杂的目标函数分解成简单的子目标函数,然后再将这些子目标函数进行协同优化。具体说来,协同优化是在优化每一子目标函数同时综合考虑其它子目标函数的结果,使子目标函数之间的优化结果能够一致。优化结果一致是指使每一变量的值在每一子目标函数的优化结果中能够一致。一般来说,可以证明,如果变量的值一致则为最优解。协同优化算法没有局部最优问题同时具有非常良好的收敛特性。它很好地解决了许多实际中非线性优化及组合优化难题。
如果目标函数是一n个变量的函数 ,简写成E(x),协同优化算法先将它分解成n个简单的子目标函数:
,简写成E(x),协同优化算法先将它分解成n个简单的子目标函数:
-
 .
.
如果单独优化每一子目标函数,则它们的结果很难达到一致。例如,变量xi在包含它的子目标函数中的最优解值很难相同。对于 ,如果我们取Ei(x)的最优解中xi的值作为该变量的值,表示成
,如果我们取Ei(x)的最优解中xi的值作为该变量的值,表示成 ,
,
-
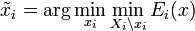 ,这里,Xi是Ei(x)的变量集,
,这里,Xi是Ei(x)的变量集, 指变量集Xi除去元素xi,
指变量集Xi除去元素xi,
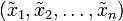 则很难为原目标函数E(x)的最优解。
则很难为原目标函数E(x)的最优解。
为了使子目标函数之间的优化结果能够一致,协同优化算法在优化每一子目标函数Ei(x)同时考虑其它子目标函数的结果,
-
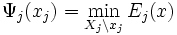 。
。
具体做法是利用其它子目标函数的优化结果通过数值加权修正每一个子目标函数如下,
-
 ,这里,λk,wij为加权系数,满足
,这里,λk,wij为加权系数,满足 。
。
然后对修正后的子目标函数进行优化,优化结果再叠代放入修正的子目标函数中。协同优化算法的叠代方程如下,
协同优化结果使每一变量的值在每一子目标函数的优化结果中达到一致。如果一致,则子目标函数的优化解既为最优解。
理论价值
现代优化理论中最重要的未解难题是发现通用的全局最优化条件。由于没有全局最优化条件,我们不知道哪里可以找到最优解,也不知道现有解是不是最优解. 因此,我们不知道如何更有效地组织优化过程及何时及时中断搜索。任何全局最优化条件既有理论意义和实用价值。协同优化算法基于一种全新的优化原理解决了这一重要问题。
理论及量子力学的关系
从协同优化算法可以推导出薛定谔方程。
假设目标能量函数为
协同优化算法在半环 上的形式为
上的形式为
如果让 及用高斯函数平滑
及用高斯函数平滑 ,则上式收敛后变成薛定谔方程如下:
,则上式收敛后变成薛定谔方程如下:
这里

薛定谔方程是物理学中最基本的方程。因此,我们可以对自然界中一般分子及蛋白分子如何形成这一非线性优化问题从全局优化的角度有进一步更深的认识。
组合最优化简介http://wenku.baidu.com/view/4b54cbbcc77da26925c5b092
数值非线性全局最优化
引言
(梯度) 或二阶导数(黑塞(Hessians)矩阵). 例如,序列二次规划方法(SQP)、增广拉格朗日方法和(非线性)内点法. 直接搜索方法不使用导数信息. 例如,Nelder-Mead、遗传算法和差分进化,以及模拟退火. 直接搜索方法往往收敛速度较慢,但可以对函数和约束条件中噪声存在的限制更为宽松.
如果收敛的话,这种算法只找到局部最优解,因此被称为 局部最优化算法. 在 Mathematica 里,局部最优化问题可以用FindMinimum 求解.
通常这种算法的计算代价更高. 全局最优化问题可以用 Minimize 精确求解或者用 NMinimize 数值化地求解.
http://reference.wolfram.com/mathematica/tutorial/ConstrainedOptimizationG
数值非线性全局最优化示例
约束最优化函数的比较
约束最优化参考文献
变分不等式简介-基本理论.数值分析及应用
增改描述、图片
作者: 韩渭敏,程晓良 编著
ISBN: 9787040208801, 7040208806
出版社: 高等教育出版社
变分不等式是一类重要的非线性问题,它们产生于许多不同领域,如物理学、工程学和金融管理科学等。本书简要地介绍了变分不等式的基本数学理论和数值方法,并给出了在力学中的一些应用。本书适合于对变分不等式基础感兴趣的数学和相关专业研究生和高年级大学生阅读。阅读本书需要有一些背景知识,如泛函分析、偏微分方程和数值分析;为完整起见在本书附录中回顾了相关的内容。
作者简介:
韩渭敏,美国爱荷华大学数学系教授。1983年毕业于复旦大学数学系。1986年在中国科学院计算中心获硕士学位。1991年在美国马里兰大学获博士学位,究范围包括计算数学、应用数学及其在工程上的应用。已发表论文约90篇,并在世界多家知名出版社出版教材和专著等十余部。
本书简要地介绍变分不等式的基本数学理论和数值方法,并给出了在力学上的一些应用。变分不等式是一类重要的非线性问题,它们产生于许多不同领域,如物理学、工程学和金融管理科学等。变分不等式始于一些力学问题的研究,早在1933年Signorini研究一个线性弹性体和刚性体的无摩擦接触问题时,就导出了被称为Signorini问题的变分不等式。本书适合于对变分不等式基础感兴趣的数学学科研究生和高年级大学生阅读。
目录:
第一章 变分不等式的引入
1.1 有限维变分不等式的例子
1.2 由变分等式到变分不等式
1.3 一些注记
第二章 椭圆型变分不等式
2.1 凸极小化问题
2.2 存在性与难一性
2.3 数值方法
2.4 一些记号及弹性体的本构关系式
2.5 一个摩擦接触问题
2.6 一个Signorini无摩擦接触问题
2.7 一个与可变形支撑的无摩擦接触问题
第三章 拟定常变分不等式
3.1 一个抽象拟定常变分不等式
3.2 空间半离散逼近格式
3.3 时间半离散逼近格式
3.4 完全离散逼近格式
3.5 若干拟定常接触问题
3.6 一个弹塑性问题
附录A 泛函分析基础
A1 Banach空间和Hilbert空间
A2 函数空间
A3 Banach不动点定理
附录B Sobolev空间
B1 弱导数
B2 Sobolev空间
B3 性质
B4 分部积分公式
B5 向量值函数空间
附录C 有限元方法
C1 有限元方法基础
C2 有限元插值的误差估计
C3 收敛性和误差估计
参考文献
名词术语
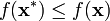
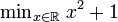
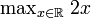
![最优化:拟牛顿法、最速下降法、共轭梯度法、信赖域法、协同优化 \operatorname{argmin}_{x\in[-\infty;-1]}\; x^2 + 1\,](http://upload.wikimedia.org/wikipedia/zh/math/6/a/6/6a68a42cae1cc2fb086bc01f024d6411.png)

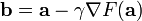

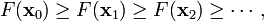
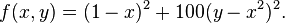
.png/350px-Gradient_ascent_(contour).png)
.png/450px-Gradient_ascent_(surface).png)