Trie结构是模式匹配中经常用到的经典结构,在字符串处理中发挥着重要的作用,比如分词算法,就会利用Trie结构将分句的已知词条先识别出来,然后再判断剩下的未识别部分是否是新的未知词。
经典的Trie结构如下图所示,

是一个典型的多叉树结构,为了保证用Trie结构进行模式匹配的效率,Trie结构的每一个节点往往会容纳输入字符集的所有字母构成的数组,以便实现高速查找,这样的缺点就是内存空间的大量浪费,因为越到Trie结构的叶节点,每个节点所包含的字母数量就越少,很可能出现为了几个字符,而多出几十个空位的情况.如上图,没有一个Trie节点的元素多于3个,但是为了算法的效率,每个节点都需要预留26个空位。读者可能会考虑对于Trie结构的每个节点,用散列表代替数组,改直接查找为散列查找,来减少空间的浪费,但是像Trie这样的基本处理工具,每秒钟可能需要对目标文本执行上万次的匹配操作,散列计算的开销很可能会成为影响程序效率的瓶颈。那么有没有既可以充分利用节点空间,又可以避免散列计算开销的Trie实现呢。Jun-Ichi
Aoe(日本)于1989年提出的double-array结构,正是将Trie结构的高效率与空间的紧凑利用相结合的理想解决方案。
前面我们提到,可以用散列表来节省Trie结构节点的空间浪费,但是我们又不想对每一次字符查找都进行散列运算,实际上,我们使用散列表的初衷,无非也就是对于当前节点,我们去哪几个节点去匹配下一个输入字符。这里我们以字符集a-z为例,来考虑如何实现Trie结构的压缩存储。

如上图所示,我们假设有一个很长的数组BASE[1...n],此时对于集合K,我们可以将BASE[1...26],作为对应的Trie结构的根节点,这样对于第1个输入字符,肯定可以映射到BASE[1...26]中的一个,然后我们将BASE[27...52]作为当第1个输入字符是a时,第2个字符对应的区间。BASE[53...78]作为当第1个字符是b时,第2个字符的映射区间,依次下去,将BASE[27...702]对应Trie结构根节点26个字母所分别对应的的第2层顶点。此时我们实现了将Trie结构的各层顶点映射到一个一维数组上面。为了能够索引到对应的BASE数组中的正确位置,我们还需要一个CHECK数组与BASE中的元素一一对应,来标记当前字符是从哪个父节点索引过来的。比如说BASE[53]的a是从BASE[2]=b索引过来的,而不是从BASE[1]或者BASE[3]索引过来的,对应于模式串前缀ba,而不是aa,ca。以上图为例,CHECK[27]到CHECK[52]的值都等于1,说明节点1是节点27-52的父节点。对于当前节点i,输入字符c,BASE与CHECK的关系是CHECK[BASE[i]+c]=i。
下面我们来看一下如何利用这种形式的Trie结构,并根据输入的模式集合,来充分利用内存空间。对于输入集合K={baby,bachelor,back,badge,badger,badness,bcs},我们会发现其对应的Trie结构的根节点只有一个合法输入b,也就是说BASE[1...26],我们只用到了一个节点BASE[2],其余25个节点都白白浪费掉了,那么我们有没有办法把这些地方复用为Trie结构的2层节点呢。字母b之后的合法输入有a,c,所以我们可以考虑找到这样的一个位置r,使得BASE[r]+a,BASE[r]+c都是还未使用的节点,这样我们就可以把r作为父节点b的2层子节点的索引位置,容易得到r=1,就满足条件,所以,我们没必要使用BASE[27...52]的空间来存放b的子节点a,c,直接使用BASE[1],BASE[3]就可以了。此时BASE[2]=0,CHECK[1]=CHECK[3]=2。同样,对于输入ba其后的合法输入有b,c,d三个,我们可以找到一个位置r令BASE[r]+b,BASE[r]+c,BASE[r]+d都为未使用节点,然后将ba之后的子节点安排在这几个位置就可以了。r=2就满足条件,此时BASE[1]=3,CHECK[3]=CHECK[4]=CHECK[5]=1。
下面给出对于模式集合K构建Double-Array的算法。
我们以例子来说明Double-Array的构建算法。模式集合K={baby,bachelor,back,badge,badger,badness,bcs},输入字符集合a-z对应数字0-25,BASE,CHECK数组均从0开始,所有单元的初始状态都为-1。另外对于BASE数组中的值,我们需要分区使用,后面会解释。这里首先要说一下独立后缀的概念,以模式集合K中的模式badness为例,其前缀b,ba,bad分别都与其他模式的前缀有重叠,而前缀badn就是模式badness的独有前缀了,所以从n到模式末尾的整个后缀ness,就是模式badness的独立后缀。对于模式串的独立后缀,我们无需将其组织在Trie结构中,而专门将其甩到另外一个结构TAIL中集中管理。
1 2 3 4 5 6 7 8 9
b a b y
b a c h e l o r
b a c k
b a d g e
b a d g e r
b a d n e s s
b c s
现在我们分层来构建集合K的Double-Array Trie结构,首先我们考察集合的第1层(也相当于所有模式串的首字母)所构成的集合S1,我们发现S1={b},此时我们在BASE数组中要找到这样的位置i对于S1的所有元素s,有BASE[i+s]=-1。对于集合S1,我们发现i=0有BASE[0+1]=BASE[1]=-1就满足条件,所以我们将CHECK[1]=-1保持不变。
接着我们来处理集合的第2层。在之后的处理中我们要注意,只有前缀相同的一组字符,我们才把他们作为一个集合来处理,相当于Trie结构的一个节点。对于本例来说,所有模式串的第1个字母都是b,我们可以得到一个集合S2={a,c},我们需要在BASE中寻找i使得BASE[i+0]=-1,BASE[i+2]=-1,此时0满足条件,我们对于集合S2的共同前缀b,找到其在BASE中对应的位置是BASE[1],所以我们令BASE[1]=0,CHECK[0]=CHECK[2]=1。这里对于满足条件的i值,我们只取满足条件的正值,但是不一定是最小的。
再接着处理第3层,此时前缀ba的直接后继字母集合S3={b,c,d},我们发现i=2可以满足BASE[3]=BASE[4]=BASE[5]=-1,此时我们用前缀ba找到其在BASE中的位置BASE[0],令BASE[0]=2,同时令CHECK[3]=CHECK[4]=CHECK[5]=0。而前缀bc的直接后继字母集合S4={s},这里我们不会将s安置在BASE数组中,因为前缀为bc的模式串只有一个bcs,所以对于模式bcs来说,前缀bc之后的部分已经形成了前面所说的独立后缀,也就是说当匹配完前缀bc之后,后面的匹配就由多模式匹配退化为目标串的与bcs的后缀s的匹配操作,此时就不需要再用Trie结构来进行查找,而直接将目标串的余下部分与s执行比较就可以了。所以我们让TAIL[1]="s"。
用上面的办法逐层处理模式集合的字符,按照公共前缀分组处理(例如公共前缀bad的后继集合S4={g,n}),遇到独立后缀,就将该独立后缀加入TAIL数组中,直到把所有模式串的独立后缀都加入到TAIL表中为止,构建Double-Array结构完毕。这里有一种情况需要特别关注,以模式badge和badger为例,badge是badger的包含前缀,当我们构建到badge尾部的时候就会出现既要索引TAIL表中的对应独立后缀(此时TAIL表的独立后缀为空串,但是依然要有),以表示一个匹配模式被发现。又要继续跳转的双重需要,此时我们可能需要对BASE值进行分区使用来兼顾这样的需求,比如将BASE值分为高16位和低16位,高16位用于索引TAIL数组,低16位用于实现跳转,当BASE值大于65535时,说明当前BASE值索引到了一个匹配模式的独立后缀,将其减去65535,所剩下的就是对应的TAIL索引。AOE的论文中是在每个模式的后面加入一个不可能字符使得任何两个模式都不存在前缀包含关系,来解决这个问题的。
上面就是逐层构建Double-Array的基本步骤,用此方法构建的Double-Array结构如图所示,由于BASE中的数值可能包含多重意思,这里将可以直接索引的模式,直接写在BASE的对应单元内,当匹配到达这些单元时,直接将输入的字符与后缀进行比较即可:
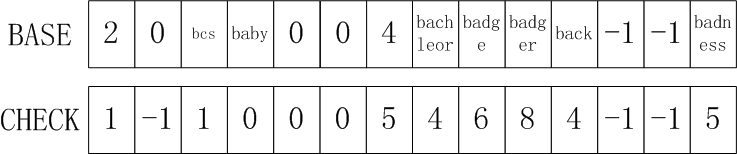
利用构建好的Double-Array匹配指定的模式的算法步骤如下。将临时变量r置为0,对于首位输入字符c,我们先要判断BASE[c]和CHECK[c],如果BASE[c]!=-1,CHECK[c]=-1,则令r=c,继续执行后续的匹配查找。如果不匹配,说明输入字母c不是Trie结构的根节点成员,放弃之。然后我们得到t= BASE[r]+c,以及CHECK[t],判断CHECK[t]是否等于r,如果不相等,则说明当前Trie节点不包含输入字母c,在模式集合中中没有该模式,所以匹配失败,否则令r=t,再继续执行上述操作。直到匹配失败,或者最终索引到TAIL中的匹配模式为止。
用上述的方法匹配模式badge的过程如下。
1)对于字母b,BASE[1]!=-1, CHECK[1]=-1,可以继续执行匹配操作, r = 1。
2)对于字母a,t=BASE[1]+a=0, CHECK[t]=CHECK[0]=1, CHECK[t]=r, r=t=0;
3)对于字母d,t=BASE[0]+d=5, CHECK[5]=0, CHECK[t]=r, r=5;
4)对于字母g,t=BASE[5]+g=6, CHECK[6]=5, CHECK[t]=r, r=6;
5)对于字母e,t=BASE[6]+e=8, CHECK[8]=badge,发现匹配。
模式ada的失败匹配过程如下
1)对于字母a,BASE[0]=2!=-1,CHECK[0]=1!=-1,所以ada不是集合中的模式,匹配终止。
模式baec的失败匹配过程如下
1)对于字母b,BASE[1]!=-1, CHECK[1]=-1,可以继续执行匹配操作, r = 1。
2)对于字母a,t=BASE[1]+a=0, CHECK[t]=CHECK[0]=1, CHECK[t]=r, r=t=0;
3)对于字母e,t=BASE[0]+e=6,CHECK[t]=CHECK[6]=5!=0,匹配失败,所以baec不是集合中的模式。
后记:
一般的算法或者数据结构,往往是时间和空间的某种妥协,如果要提高运行效率,往往需要一些额外的内存空间,反之亦然。而Double-Array之于Trie结构,就好像是一种完美的诠释,在实现了对Trie结构空间的充分利用的同时,又不牺牲查找速度,那么是不是Double-Array就无懈可击了呢。当然不是。要驾驭这种优美结构的代价,就是实现Double-Array的高复杂性,以及在Double-Array中插入,修改,删除单条数据的高代价。AOE在论文中详细介绍了Double-Array的增加,变更,删除条目的操作算法,相较于通俗的Trie实现,要复杂的多得多,本文我也仅仅是将自己对Double-Array的一点浅显理解写出来而已,实际上Double-Array是一个相当复杂的数据结构,他只能在某些应用场合替代普通的Trie结构,以后如果条件允许,我还会将Double-Array的更多细节一一介绍。
An Implementation of Double-Array Trie
Contents
- What is Trie?
- What Does It Take to Implement a Trie?
- Tripple-Array Trie
- Double-Array Trie
- Suffix Compression
- Key Insertion
- Key Deletion
- Double-Array Pool Allocation
- An Implementation
- Download
- Other Implementations
- References
What is Trie?
Trie is a kind of digital search tree. (See [Knuth1972] for the detail of digital search tree.) [Fredkin1960] introduced
the trie terminology, which is abbreviated from "Retrieval".
Trie is an efficient indexing method. It is indeed also a kind of deterministic finite automaton (DFA) (See [Cohen1990], for example, for the definition of DFA). Within
the tree structure, each node corresponds to a DFA state, each (directed) labeled edge from a parent node to a child node corresponds to a DFA transition. The traversal starts at the root node. Then, from head to tail, one by one character in the key string
is taken to determine the next state to go. The edge labeled with the same character is chosen to walk. Notice that each step of such walking consumes one character from the key and descends one step down the tree. If the key is exhausted and a leaf node is
reached, then we arrive at the exit for that key. If we get stuck at some node, either because there is no branch labeled with the current character we have or because the key is exhausted at an internal node, then it simply implies that the key is not recognized
by the trie.
Notice that the time needed to traverse from the root to the leaf is not dependent on the size of the database, but is proportional to the length of the key. Therefore, it is usually much faster than B-tree or any comparison-based indexing method in general
cases. Its time complexity is comparable with hashing techniques.
In addition to the efficiency, trie also provides flexibility in searching for the closest path in case that the key is misspelled. For example, by skipping a certain character in the key while walking, we can fix the insertion kind of typo. By walking toward
all the immediate children of one node without consuming a character from the key, we can fix the deletion typo, or even substitution typo if we just drop the key character that has no branch to go and descend to all the immediate children of the current node.
What Does It Take to Implement a Trie?
In general, a DFA is represented with a transition table, in which the rows correspond to the states, and the columns correspond to the transition labels. The data kept in each cell is then the next state to go for a given state when the input
is equal to the label.
This is an efficient method for the traversal, because every transition can be calculated by two-dimensional array indexing. However, in term of space usage, this is rather extravagant, because, in the case of trie, most nodes have only a few branches, leaving
the majority of the table cells blanks.
Meanwhile, a more compact scheme is to use a linked list to store the transitions out of each state. But this results in slower access, due to the linear search.
Hence, table compression techniques which still allows fast access have been devised to solve the problem.
- [Johnson1975] (Also explained in [Aho+1985] pp.
144-146) represented DFA with four arrays, which can be simplified to three in case of trie. The transition table rows are allocated in overlapping manner, allowing the free cells to be used by other rows. - [Aoe1989] proposed an improvement from the three-array structure by reducing the arrays to two.
Tripple-Array Trie
As explained in [Aho+1985] pp. 144-146, a DFA compression could be done using four linear arrays, namely default, base, next,
and check. However, in a case simpler than the lexical analyzer, such as the mere trie for information retrieval, the default array could be omitted. Thus, a trie can be implemented using three arrays according to this scheme.
Structure
The tripple-array structure is composed of:
- base. Each element in base corresponds to a node of the trie. For a trie node s, base[s] is the starting index within the next and check pool (to be
explained later) for the row of the node s in the transition table. - next. This array, in coordination with check, provides a pool for the allocation of the sparse vectors for the rows in the trie transition table. The vector data, that is, the vector of transitions from every node,
would be stored in this array. - check. This array works in parallel to next. It marks the owner of every cell in next. This allows the cells next to one another to be allocated to different trie nodes. That means the sparse vectors of
transitions from more than one node are allowed to be overlapped.
Definition 1. For a transition from state s to t which takes character c as the input, the condition maintained in the tripple-array trie is:
check[base[s] + c] = s
next[base[s] + c] = t
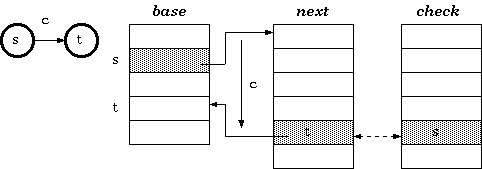
Walking
According to definition 1, the walking algorithm for a given state s and the input character c is:
if check[t] = s
then next state := next[t]
else fail endif
Construction
To insert a transition that takes character c to traverse from a state s to another state t, the cell next[base[s] + c]] must be managed to be available. If it is already
vacant, we are lucky. Otherwise, either the entire transition vector for the current owner of the cell or that of the state sitself must be relocated. The estimated cost for each case could determine which one to move. After finding the free slots
to place the vector, the transition vector must be recalculated as follows. Assuming the new place begins at b, the procedure for the relocation is:
state; b : base_index){ Move base for state
s to a new place beginning at b }begin foreach input character
c for the state s { i.e. foreach
c such that check[base[s] + c]] =
s } begin check[b +
c] := s; { mark owner }
next[b + c] := next[base[s] +
c]; { copy data } check[base[s] +
c] := none { free the cell }
end; base[s] := bend
Double-Array Trie
The tripple-array structure for implementing trie appears to be well defined, but is still not practical to keep in a single file. The next/check pool may be able to keep in a single array of integer couples, but the base array
does not grow in parallel to the pool, and is therefore usually split.
To solve this problem, [Aoe1989] reduced the structure into two parallel arrays. In the double-array structure, the base and next are
merged, resulting in only two parallel arrays, namely, base and check.
Structure
Instead of indirectly referencing through state numbers as in tripple-array trie, nodes in double-array trie are linked directly within the base/checkpool.
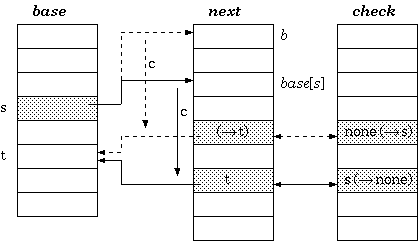
Definition 2. For a transition from state s to t which takes character c as the input, the condition maintained in the double-array trie is:
check[base[s] + c] = s
base[s] + c = t
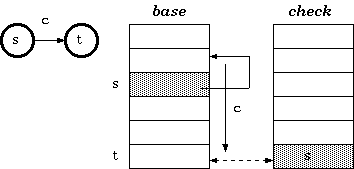
Walking
According to definition 2, the walking algorithm for a given state s and the input character c is:
if check[t] = s
then next state := t else
fail endif
Construction
The construction of double-array trie is in principle the same as that of tripple-array trie. The difference is the base relocation:
state; b : base_index){ Move base for state
s to a new place beginning at b }begin foreach input character
c for the state s { i.e. foreach
c such that check[base[s] + c]] =
s } begin check[b +
c] := s; { mark owner }
base[b + c] := base[base[s] +
c]; { copy data }
{ the node base[s] + c is to be moved to
b + c; Hence, for any i for which check[i] =
base[s] + c, update check[i] to
b + c } foreach input character
d for the node base[s] + c
begin check[base[base[s] +
c] + d] := b + c end;
check[base[s] + c] :=
none { free the cell } end;
base[s] := bend
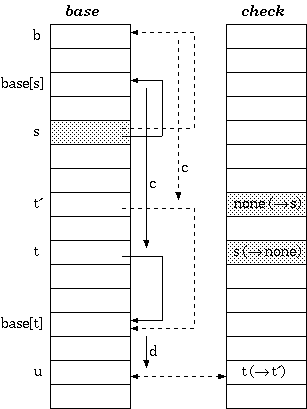
Suffix Compression
[Aoe1989] also suggested a storage compression strategy, by splitting non-branching suffixes into single string storages, called tail, so that the rest
non-branching steps are reduced into mere string comparison.
With the two separate data structures, double-array branches and suffix-spool tail, key insertion and deletion algorithms must be modified accordingly.
Key Insertion
To insert a new key, the branching position can be found by traversing the trie with the key one by one character until it gets stuck. The state where there is no branch to go is the very place to insert a new edge, labeled by the failing character. However,
with the branch-tail structure, the insertion point can be either in the branch or in the tail.
1. When the branching point is in the double-array structure
Suppose that the new key is a string a1a2...ah-1ahah+1...an, where a1a2...ah-1 traverses the trie from the root to a node sr in the double-array structure,
and there is no edge labeled ah that goes out of sr. The algorithm called A_INSERT in [Aoe1989] does as follows:
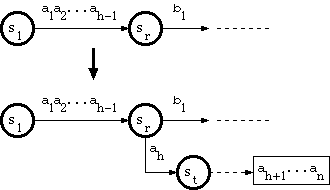
2. When the branching point is in the tail pool
Since the path through a tail string has no branch, and therefore corresponds to exactly one key, suppose that the key corresponding to the tail is
a1a2...ah-1ah...ah+k-1b1...bm,
where a1a2...ah-1 is in double-array structure, and ah...ah+k-1b1...bm is in tail. Suppose that the substring a1a2...ah-1 traverses the trie from the
root to a node sr.
And suppose that the new key is in the form
a1a2...ah-1ah...ah+k-1ah+k...an,
where ah+k <> b1. The algorithm called B_INSERT in [Aoe1989] does as follows:
in tail pool;From st, insert edge labeled ah+k to new node sv;Let sv be separate node pointing to a string ah+k+1...an in tail pool.
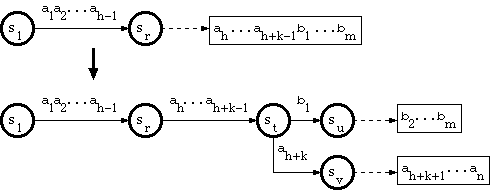
Key Deletion
To delete a key from the trie, all we need to do is delete the tail block occupied by the key, and all double-array nodes belonging exclusively to the key, without touching any node belonging to other keys.
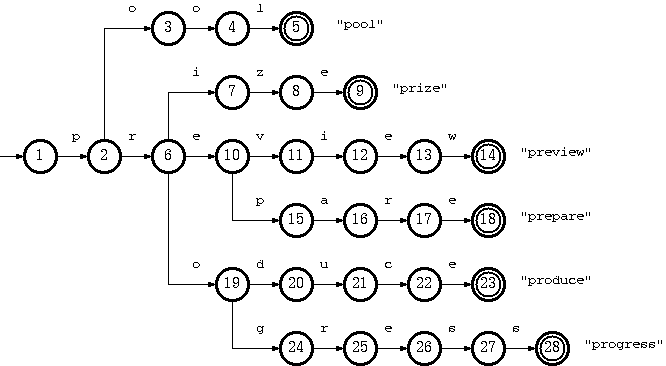
Consider a trie which accepts a language K = {pool#, prepare#, preview#, prize#, produce#, producer#, progress#} :
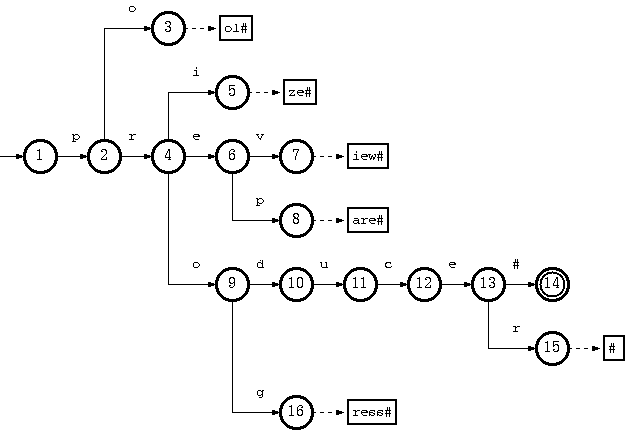
The key "pool#" can be deleted by removing the tail string "ol#" from the tail pool, and node 3 from the double-array structure. This is the simplest case.
To remove the key "produce#", it is sufficient to delete node 14 from the double-array structure. But the resulting trie will not obay the convention that every node in the double-array structure, except the separate nodes which point to tail blocks, must belong
to more than one key. The path from node 10 on will belong solely to the key "producer#".
But there is no harm violating this rule. The only drawback is the uncompactnesss of the trie. Traversal, insertion and deletion algoritms are intact. Therefore, this should be relaxed, for the sake of simplicity and efficiency of the deletion algorithm. Otherwise,
there must be extra steps to examine other keys in the same subtree ("producer#" for the deletion of "produce#") if any node needs to be moved from the double-array structure to tail pool.
Suppose further that having removed "produce#" as such (by removing only node 14), we also need to remove "producer#" from the trie. What we have to do is remove string "#" from tail, and remove nodes 15, 13, 12, 11, 10 (which now belong solely to the key "producer#")
from the double-array structure.
We can thus summarize the algorithm to delete a key k = a1a2...ah-1ah...an, where a1a2...ah-1 is in double-array structure, and ah...an is in tail
pool, as follows :
sr;repeat p := parent of
s; Delete node s from double-array structure; s :=
puntil s = root or
outdegree(s) > 0.
Where outdegree(s) is the number of children nodes of s.
Double-Array Pool Allocation
When inserting a new branch for a node, it is possible that the array element for the new branch has already been allocated to another node. In that case, relocation is needed. The efficiency-critical part then turns out to be the search for a new place. A
brute force algoritm iterates along the checkarray to find an empty cell to place the first branch, and then assure that there are empty cells for all other branches as well. The time used is therefore proportional to the size of the double-array
pool and the size of the alphabet.
Suppose that there are n nodes in the trie, and the alphabet is of size m. The size of the double-array structure would be n + cm, where c is a coefficient which is dependent on the characteristic
of the trie. And the time complexity of the brute force algorithm would be O(nm + cm2).
[Aoe1989] proposed a free-space list in the double-array structure to make the time complexity independent of the size of the trie, but dependent on the number of the
free cells only. The check array for the free cells are redefined to keep a pointer to the next free cell (called G-link) :
Definition 3. Let r1, r2, ... , rcm be the free cells in the double-array structure, ordered by position. G-link is defined as follows :
check[0] = -r1
check[ri] = -ri+1 ; 1 <= i <= cm-1
check[rcm] = -1
By this definition, negative check means unoccupied in the same sense as that for "none" check in the ordinary algorithm. This encoding scheme forms a singly-linked list of free cells. When searching for an empty cell, only cm free
cells are visited, instead of all n + cm cells as in the brute force algorithm.
This, however, can still be improved. Notice that for those cells with negative check, the corresponding base's are not given any definition. Therefore, in our implementation, Aoe's G-link is modified to be doubly-linked list by letting base of
every free cell points to a previous free cell. This can speed up the insertion and deletion processes. And, for convenience in referencing the list head and tail, we let the list be circular. The zeroth node is dedicated to be the entry point of the list.
And the root node of the trie will begin with cell number one.
Definition 4. Let r1, r2, ... , rcm be the free cells in the double-array structure, ordered by position. G-link is defined as follows :
check[0] = -r1
check[ri] = -ri+1 ; 1 <= i <= cm-1
check[rcm] = 0
base[0] = -rcm
base[r1] = 0
base[ri+1] = -ri ; 1 <= i <= cm-1
Then, the searching for the slots for a node with input symbol set P = {c1, c2, ..., cp} needs to iterate only the cells with negative check :
and s <= c1do s := -check[s]end;if s = 0
then return FAIL; {or reserve some additional space}{continue searching for the row, given that s matches c1}while s <> 0
do i := 2; while i <= p
and check[s + ci - c1] < 0
do i := i + 1 end; if i = p + 1
then return s - c1; {all cells required are free, so return it} s := -check[s]end;return
FAIL; {or reserve some additional space}
The time complexity for free slot searching is reduced to O(cm2). The relocation stage takes O(m2). The total time complexity is therefore O(cm2 + m2) = O(cm2).
It is useful to keep the free list ordered by position, so that the access through the array becomes more sequential. This would be beneficial when the trie is stored in a disk file or virtual memory, because the disk caching or page swapping would be used
more efficiently. So, the free cell reusing should maintain this strategy :
and t < s do t := -check[t]end;{t now points to the cell after s' place}check[s] := -t;check[-base[t]]
:= -s;base[s] := base[t];base[t] := -s;
Time complexity of freeing a cell is thus O(cm).
An Implementation
In my implementation, I designed the API with persistent data in mind. Tries can be saved to disk and loaded for use afterward. And in newer versions, non-persistent usage is also possible. You can create a trie in memory, populate data to it, use it, and free
it, without any disk I/O. Alternatively you can load a trie from disk and save it to disk whenever you want.
The trie data is portable across platforms. The byte order in the disk is always little-endian, and is read correctly on either little-endian or big-endian systems.
Trie index is 32-bit signed integer. This allows 2,147,483,646 (231 - 2) total nodes in the trie data, which should be sufficient for most problem domains. And each data entry can store a 32-bit integer value associated to it. This value can be used
for any purpose, up to your needs. If you don't need to use it, just store some dummy value.
For sparse data compactness, the trie alphabet set should be continuous, but that is usually not the case in general character sets. Therefore, a map between the input character and the low-level alphabet set for the trie is created in the middle. You will
have to define your input character set by listing their continuous ranges of character codes in a .abm (alphabet map) file when creating a trie. Then, each character will be automatically assigned internal codes of continuous values.
Download
Update: The double-array trie implementation has been simplified and rewritten from scratch in C, and is now named libdatrie. It is now available under the terms of GNU
Lesser General Public License (LGPL):
- libdatrie-0.2.4 (30 June 2010)
- libdatrie-0.2.3 (27 February 2010)
- libdatrie-0.2.2 (29 April 2009)
- libdatrie-0.2.1 (5 April 2009)
- libdatrie-0.2.0 (24 March 2009)
- libdatrie-0.1.3 (28 January 2008)
- libdatrie-0.1.2 (25 August 2007)
- libdatrie-0.1.1 (12 October 2006)
- libdatrie-0.1.0 (18 September 2006)
SVN: svn co http://linux.thai.net/svn/software/datrie
The old C++ source code below is under the terms of GNU Lesser General Public License (LGPL):
- midatrie-0.3.3 (2 October 2001)
- midatrie-0.3.3 (16 July 2001)
- midatrie-0.3.2 (21 May 2001)
- midatrie-0.3.1 (8 May 2001)
- midatrie-0.3.0 (23 Mar 2001)
Other Implementations
- DoubleArrayTrie: Java implementation by Christos Gioran (More
information)
References
- [Knuth1972] Knuth, D. E. The Art of Computer Programming Vol. 3, Sorting and Searching. Addison-Wesley. 1972.
- [Fredkin1960] Fredkin, E. Trie Memory. Communication of the ACM. Vol. 3:9 (Sep 1960). pp. 490-499.
- [Cohen1990] Cohen, D. Introduction to Theory of Computing. John Wiley & Sons. 1990.
- [Johnson1975] Johnson, S. C. YACC-Yet another compiler-compiler. Bell Lab. NJ. Computing Science Technical Report 32. pp.1-34. 1975.
- [Aho+1985] Aho, A. V., Sethi, R., Ullman, J. D. Compilers : Principles, Techniques, and Tools. Addison-Wesley. 1985.
- [Aoe1989] Aoe, J. An Efficient Digital Search Algorithm by Using a Double-Array Structure. IEEE Transactions on Software Engineering. Vol. 15, 9 (Sep 1989).
pp. 1066-1077. - [Virach+1993] Virach Sornlertlamvanich, Apichit Pittayaratsophon, Kriangchai Chansaenwilai. Thai Dictionary Data Base Manipulation using Multi-indexed Double Array Trie. 5th
Annual Conference. National Electronics and Computer Technology Center. Bangkok. 1993. pp 197-206. (in Thai)
Copyright © 1999 by Theppitak Karoonboonyanan, Software and Language Engineering Laboratory, National Electronics and Computer Technology Center. All rights reserved.
Copyright © 2003-2010 by Theppitak Karoonboonyanan. All rights reserved.