学步园

pku 2154 Color
   burnside是一种计数方法，用来计算含有不等价类的数量， 简单说就是对于每个置换 fi ，他都对一定量的着色无效（该着色经过fi置换不变），设这些着色数量为ai，  所有ai的平均数就是不等价类的数量， 当然也可以变换求和顺序， 先考虑每中着色， 再求他的稳定核，
但一般情况是置换数很少， 着色数很多， 所以前者很常用
   这道题是比较经典的循环排列计数，有 N 个置换{ P^0 = r, P^1, P^2, P^(n-1)} r为单位置换
   写个小程序观察 ，发现 P^x 的循环结恰好是gcd（x , N）

   这样我们就有一个较好的求和式子 ：
                                       
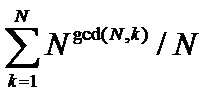
   但N可到10^9，这个求和式直接用不现实，继续观察，发现这些数都是N的约数，自然会想改变求和顺序，先考虑每个约数，我又写了个小程序输出每个约数的数量（一开始就知道他大概跟欧拉数有关系，但没有发现明显的积性），打出表来一看，原来因子x的数量是Phi（N/x）；这样式子就变成了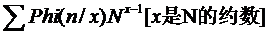                    

     φ(N/pi)就是
1 -- N 中所有满足gcd(i,N)=pi 的 i 的个数
                      (Hint gcd（i,N）=pi 等价于 gcd(i/pi,N/pi)=1 )

   要约数尽量的多，就要不同的素因子尽量多，N最多不会有10个不同的素因子，约数不会超过1024个，而且约数越多，约数就会变小，求约数的欧拉数虽然是O( sqrt(N) )的，但需要对于其中一个约数计算超过20次的不会超过3个，有了这些估计，虽然具体的算法复杂度不知道，
我决定冒险试试，应该不会超时。结果跑了600ms，还是比较理想的

1.裸polya，c中颜色，n个元素，旋转和对称同构有多少种？

http://acm.hdu.edu.cn/showproblem.php?pid=3923

#include<iostream>
#include<stdio.h>
using namespace std;
typedef long long LL;
const LL mod=1000000007;
const int N=10050;
LL p[N];
LL exgcd(LL a,LL b,LL &x,LL &y)
{
    if(b==0){
        x=1; y=0;
        return a;
    }
    LL ret=exgcd(b,a%b,x,y);
    LL tmp=x; x=y;
    y=tmp-a/b*y;
    y=(y%mod+mod)%mod;
    return ret;
}
LL gcd(LL a,LL b){ return b?gcd(b,a%b):a; }
LL polya(LL c,int n)
{
    LL ret=0;
    p[0]=1;
    for(int i=1;i<=n;i++)
        p[i]=p[i-1]*c%mod;
    //旋转
    for(int i=1;i<=n;i++){
        ret=(ret+p[gcd(i,n)])%mod;
//        cout<<"zhuan "<<ret<<endl;
    }
    //翻转
    if(n&1){
        ret=(ret+n*p[n/2+1])%mod;
    }
    else{
        ret=(ret+n/2*p[n/2])%mod;
        ret=(ret+n/2*p[n/2+1])%mod;
    }
    LL x,y;
    exgcd(2ll*n,mod,x,y);
//    cout<<ret<<' '<<x<<endl;
    ret=ret*x%mod;
    return ret;
}
int main()
{
    int t;
    scanf("%d",&t);
    for(int cas=1;cas<=t;cas++)
    {
        int c,n;
        scanf("%d%d",&c,&n);
        printf("Case #%d: %d\n",cas,(int)polya(c,n));
    }
    return 0;
}