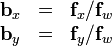From：维基百科。
透视投影的定义可以理解为透过摄像机取景器对于被投影物体进行观察。摄像机的位置、朝向和视野都将影响投影变换的结果。我们定义以下变量来对这一变换进行描述：
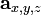：将被投影的三维空间中的点。
：摄像机的位置。
：摄像机的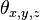旋转角度。（也可以理解为物体的旋转角度，但是方向相反,注意角度是绕x、y、z的旋转度数而不是与x、y、z的夹角！）- 当 =<0,0,0>且 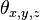=<0,0,0>,
三维向量<1,2,0>将被投影到二维向量<1,2>。 
：观测者相对显示平面的位置。
最终结果为：
：
所产生的二维投影。
首先我们定义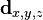点
作为点向摄像机坐标系所作的变换，其中摄像机坐标系由摄像机的位置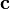
和旋转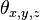所决定。该过程为：先用减去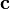(平移)，然后使用由
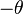（旋转方向为逆时针，所以成像方向要加负号）产生的旋转矩阵乘上该结果。
该变换通常称为摄像机变换(注意该计算过程假设使用左手法则)：
或者使用以下这种非矩阵表示的形式，其中角度的正负号与矩阵表示形式不同：
然后将变换后的该点通过以下方程投影到二维平面（此处投影平面为x/y平面，有时也使用x/z）:
（假设摄像机和人眼同处一个位置，Ez/Dz = 1）
或在齐次坐标系下可以表示为：
和
观测者到显示平面的距离，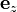
，直接关系到视野的大小。
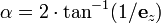为可视角度。（这里假设屏幕的两角为(-1,-1)和(1,1)）
如果要在一些特定的显示设备上显示该二维平面，之后还要进行一些必要的剪裁和缩放操作。
图示
计算三维空间中位于Ax，Az的点在屏幕坐标x轴的位置：
对于y轴同样有:
(其中Ax和Ay是透视转换前物体在空间中的坐标)