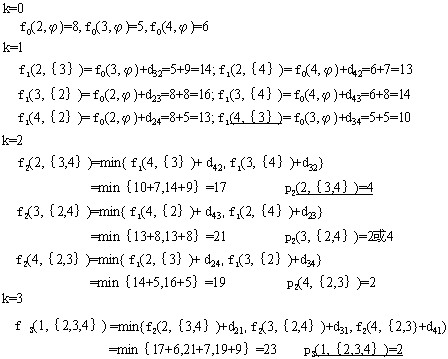一,问题由来
货郎担问题也叫旅行商问题,即TSP问题(Traveling Salesman Problem),是数学领域中著名问题之一。
二,问题描述
1)货郎担问题提法:有n个城市,用1,2,…,n表示,城i,j之间的距离为dij,有一个货郎从城1出发到其他城市一次且仅一次,最后回到城市1,怎样选择行走路线使总路程最短?
2)旅行商问题的提法:假设有一个旅行商人要拜访n个城市,他必须选择所要走的路径,路经的限制是每个城市只能拜访一次,而且最后要回到原来出发的城市。路径的选择目标是要求得的路径路程为所有路径之中的最小值。
三,问题求解
1)动态规划解
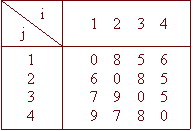
例题: 设v1,v2,……..,vn是已知的n个城镇,城镇vi到城镇vj的距离为dij,现求从v1出发,经各城镇一次且仅一次返回v1的最短路程。

分析:设S表示从v1到vi中间所可能经过的城市集合,S实际上是包含除v1和vi两个点之外的其余点的集合,但S中的点的个数要随阶段数改变。
建模:状态变量(i,S)表示:从v1点出发,经过S集合中所有点一次最后到达vi。
最优指标函数fk(i,S)为从v1出发,经过S集合中所有点一次最后到达vi。
决策变量Pk(i,S)表示:从v1经k个中间城镇的S集合到vi城镇的最短路线上邻接vi的前一个城镇,则动态规划的顺序递推关系为:
fk(i,S)= min{ fk-1(j,S、{ j }+dji} j属于S
f0(i,空集)=d1i (k=1,2,…,n-1,i=2,3,…n)
求解:K=0
f0(2,空集)=d12=6
f0(3,空集)=d13=7
f0(4,空集)=d14=9
当k=1时:
从城市V1出发,经过1个城镇到达Vi的最短距离为:
f1(2,{ 3 }) = f0 (3,空)+d 32 =7+8=15
f1(2,{ 4 }) = f0 (4,空)+d 42 =9+8=14
f1(3,{ 2 }) = f0 (2,空)+d 23 =6+9=15
f1(3,{ 4 }) = f0 (4,空)+d 43 =9+5=14
f1(4,{ 2 }) = f0 (2,空)+d 24 =6+7=13
f1(4,{ 3 }) = f0 (3,空)+d 34 =7+8=15
当k=2时,
从城市V1出发,中间经过2个城镇到达Vi的最短距离.
f2(2,{ 3,4 }) = min[ f1(3,{4})+d32, f1(4,{3})+ d42] =min[14+8,15+5]=20
P2(2,{3,4})=4
f2(3,{ 2,4 })= min[14+9,13+5]=18
P2(3,{2,4})=4
f2(4,{ 2,3})= min[15+7,15+8]=22
P2(4,{2,3})=2
当k=3时:
从城市V1出发,中间经过3个城镇最终回到Vi的最短距离.
f3(1,{ 2,3,4 })= min[f2(2,{
3,4 }) + d 21,f2(3,{ 2,4})+ d31,f2(4,{
2,3 }) + d41]=min[20+8,18+5,22+6]=23
P3(1,{2,3,4})=3
逆推回去,货郎的最短路线是1 2
4 3 1,最短距离为23.
四,源码
- #include<iostream>
- #include<iomanip>
- using namespace std;
- int n;
- int cost[20][20]={};
- bool done[20]={1};
- int start = 0; //从城市0开始
- int imin(int num, int cur)
- {
- if(num==1) //递归调用的出口
- return cost[cur][start]; //所有节点的最后一个节点,最后返回 最后一个节点到起点的路径
- int mincost = 10000;
- for(int i=0; i<n; i++)
- {
- cout<<i<<" i:"<<done[i]<<endl;
- if(!done[i] && i!=start) //该结点没加入 且 非起始点
- {
- if(mincost <= cost[cur][i]+cost[i][start])
- {
- continue; //其作用为结束本次循环。即跳出循环体中下面尚未执行的语句。区别于break
- }
- done[i] = 1; //递归调用时,防止重复调用
- int value = cost[cur][i] + imin(num-1, i);
- if(mincost > value)
- {
- mincost = value;
- }
- done[i] = 0;//本次递归调用完毕,让下次递归调用
- }
- }
- return mincost;
- }
- int main()
- {
- // cin >> n;
- n=4;
- int cc[4][4]={{0 ,4, 1, 3},
- {4 ,0 ,2, 1},
- {1 ,2 ,0, 5},
- {3 ,1, 5, 0}};
- for(int i=0; i<n; i++)
- {
- for(int j=0; j<n; j++)
- {
- //cin >> cost[i][j];
- cost[i][j]=cc[i][j];
- }
- }
- cout << imin(n, start) << endl;
- return 0;
- }
源码解析:核心是动态规划,自底向上的思想。
写法是递归写法,自顶向下递归调用。
第一次调用:起点0,第一个节点是1时候
{
进入递归---->value = d01 +imin(3,1)
{
进入递归-----value = d12 +imin(2,2)
{
进入递归---->value = d23 +imin(1,3)
{
进入递归---->return d30;
}
……}
……}
……}
转载自:http://blog.csdn.net/tianshuai1111/article/details/7535026
运筹学中的处理
| 货郎担问题也称旅行员问题,是运筹学里一个著名问题。设有n个城市,以1,2,…,n表示, |
|
| 规定推销员是从城市1出发,设推销员走到i城,s表示到达i城之前中途所经过的城市集合。选取(i,s)作为描述过程的状态变量,定义 边界条件为 |
|
| 其中N1表示从1城出发回到1城的所有中间城市集合。 | |
|
|
解:
|
|
| 由此可知,推销员最短路线为 1→3→4→2→1 ,最短距离为23。 | |
| 实际中很多问题都可以归结为货郎担问题,如物资运输中汽车应走怎样的路线使路程最短;工厂中机床应如何布置,可使零件所经过的路线最短等等。 |