上学的时候汇编语言中有原码、反码、补码。
考试的时候经常考,比较好的办法就是记住他们的转换规则,但是虽然记住转换规则,考试也考不差,心头却始终有朵乌云挥之不去,令人异常纠结,夜不能寐,食不甘味,却还抓不住,不知道怎么解决才好。
比如正数1八位字节表示是00000001,负数-1的八位字节表示是10000001这种表示是原码。最高位为符号位,0表示正,1表示负。
00000001反码00000001补码00000001 正数的反码和补码和原码一样
10000001反码11111110补码11111111 负数的反码除符号位其余各位取反;补码在反码基础上加1
为什么要发明出反码和补码呢?(反码没仔细查考)内容来自维基百科。
补码系统的最大优点是可以在加法或减法处理中,不需因为数字的正负而使用不同的计算方式。只要一种加法电路就可以处理各种有号数加法,而且减法可以用一个数加上另一个数的补码来表示,因此只要有加法电路及补码电路即可完成各种有号数加法及减法,在电路设计上相当方便。
补码的工作原理
学习计算机科学的学生会问:为什么补码能这么巧妙实现了正负数的加减运算?答案是:指定n比特字长,那么就只有2n个可能的值,加减法运算都存在上溢出与下溢出的情况,实际上都等价于模2n的加减法运算。这对于n比特无符号整数类型或是n比特有符号整数类型都同样适用。
例如,8位无符号整数的值的范围是0到255. 因此4+254将上溢出,结果是2,即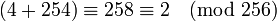 。
。
例如,8位有符号整数的值的范围,如果规定为−128到127, 则126+125将上溢出,结果是−5,即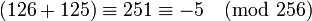 。
。
对于8位字长的有符号整数类型,以28即256为模,则
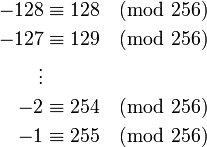
所以模256下的加减法,用0, 1, 2, …, 254,255表示其值,或者用−128, −127,… , −1, 0, 1, 2,… ,127是完全等价的。−128与128,−127与129,…,−2与254,−1与255可以互换而加减法的结果不变。从而,把8位(octet)的高半部分(即二进制的1000 0000到1111 1111)解释为−128到−1,同样也实现了模256的加减法,而且所需要的CPU加法运算器的电路实现与8位无符号整数并无不同。
实际上对于8比特的存储单元,把它的取值[00000000, …, 11111111]解释为[0, 255], 或者[-1, 254], 或者[-2, 253], 或者[-128, 127], 或者[-200, 55], 甚至或者[500, 755], 对于加法硬件实现并无不同。