现在的位置: 首页 > 综合 > 正文

压缩感知（Compressed sensing）from wiki

2019年03月16日 ⁄ 综合 ⁄ 共 3626字 ⁄ 字号小中大 ⁄ 评论关闭

压缩感知（Compressed sensing），也被称为压缩采样（Compressive sampling）或稀疏采样（Sparse sampling），是一种寻找欠定线性系统的稀疏解的技术。压缩感知被应用于电子工程尤其是信号处理中，用于获取和重构稀疏或可压缩的信号。這個方法用到訊號稀疏的特性，得以從相對較少的測量值還原出原來整個欲得知的訊號。MRI就是一個可能使用此方法的應用。这一方法至少已经存在了四十年，由于David
Donoho、Emmanuel Candès和陶哲轩的工作，最近这个领域有了长足的发展。

概览

信号处理领域中的一个常见问题就是从一系列的采样中重建原本的信号。大致而言，由于不可能重建出未被采样的部分信号，这一任务是无法完全实现的。然而通过借助对于信号（性质）的预先了解或合理假设，完美地通过一系列采样重建原信号就成为了可能。随着科学的发展，数学家们逐步增进了如何作出合理假设的能力，并慢慢了解到在何种情况下可将这些假设一般化、推广化。

信号处理领域中的一次较早的突破是采样定理的提出。这一定理证明了若信号的最高频率小于采样频率的一半，便可完美地从采样结果中恢复原本信号。

在2004年左右，Emmanuel Candès、陶哲轩和David
Donoho证明了在已知信号稀疏性的情况下，可能凭借较采样定理所规定更少的采样数重建原信号。这一理论也是压缩感知的基石。

取样方法

在理论上，为了确保信号重建的准确度，需要令所采用的取样矩阵各行列之间相干性（[[:en:Coherence_(signal_processing)}]]）尽量地低，且须矩阵元素（element）取值随机性尽量地高。

考虑到以上原因，最为标准的做法是采用相同独立分布随机高斯矩阵（identical independent distributed random Gaussian matrix）对待处理信号进行取样，即可确保在信号具有足够稀疏性的前提下得到较佳的压缩感知重建效果。

但是在采用相同独立分布随机高斯矩阵时，所需要的数据存储量过于庞大——每个矩阵元素都要单独记录，且数据类型一般为浮点数——这就促进了简化取样矩阵的研究；目前被提出的简化取样矩阵主要包括两种：结构简化采样矩阵与数值简化采样矩阵。

结构简化采样矩阵

一种基本的结构简化采样矩阵是Toeplitz矩阵：

$A =\begin{bmatrix} a_{0} & a_{-1} & a_{-2} & \ldots & \ldots &a_{-n+1} \\ a_{1} & a_0 & a_{-1} & \ddots & & \vdots \\ a_{2} & a_{1} & \ddots & \ddots & \ddots& \vdots \\ \vdots & \ddots & \ddots & \ddots & a_{-1} & a_{-2}\\ \vdots & & \ddots & a_{1} & a_{0}& a_{-1} \\a_{n-1} & \ldots & \ldots & a_{2} & a_{1} & a_{0}\end{bmatrix}$ ，

其中 $A_{i,j} = A_{i+1,j+1} = a_{i-j}.\$ 。

在采用Toeplitz矩阵进行压缩感知取样时，便可以只在系统内存中储存第一行与第一列的矩阵元素，大大降低了储存成本，为算法的硬件实现降低了门槛。

数值简化采样矩阵

数值简化采样矩阵普遍将原有的、按照高斯分布随机取值的采样矩阵元素以数值上更为简单的元素取代，但在分布上维持矩阵元素的分布随机性——即缩减了储存浮点数这一方面的成本。

一种较为基本的数值简化采样矩阵是0-1伯努利矩阵，其中的元素仅有0和1两种，分布模式为相同独立的伯努利分布（identical
independent Bernoulli distribution）。

对于每一个矩阵元素，该分布的概率质量函数 $f$ 为：
$f(k;p) = \begin{cases} p & \text{if }k=1, \\[6pt]1-p & \text {if }k=0.\end{cases}$

欠定线性系统

如果一个线性方程组未知数的数目超过方程的数目，这个方程组被称为欠定，并且一般而言有无数个解。但是，如果这个欠定系统只有唯一一个稀疏解，那么我们可以利用压缩感知理论和方法来寻找这个解。值得注意的是，不是所有欠定线性方程组都有稀疏解。

求解/重构方法

压缩感知利用了很多信号中所存在的冗余（换言之，这些信号并非完全是噪声）。具体而言，很多信号都是“稀疏”的；在适当的表示域中，它们的很多系数都是等于或约等于零。

在信号获取阶段，压缩感知在信号并不稀疏的域对信号进行线性测量。

为了从线性测量中重构出原来的信号，压缩感知求解一个称为L1-范数正则化的最小二乘问题。从理论上可以证明，在某些条件下，这个正则化最小二乘问题的解正是原欠定线性系统的稀疏解。

基追踪

基追踪（basis pursuit[1]）是一种信号重建演算法，被广泛地用于压缩感知领域，属于数学最优化问题的范畴，形式为
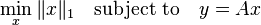$\min_x \|x\|_1 \quad \mbox{subject to} \quad y = Ax$ 。，

其中x是N×1尺寸向量，表示输出（信号），y是M×1的测量向量，A是M × N的“转换矩阵”或曰“测量矩阵”；其中M < N。

基追踪常在需要完美满足欠定线性方程组系统中y = Ax时被应用，且要求解在L₁基准下为最稀疏的。

若应用情景允许降低对完美恢复的要求，以换取更加稀疏的解x，降噪基追踪（basis
pursuit denoising[2]）更为适用。

匹配追踪

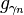匹配追踪（Matching pursuit[3]）是一种稀疏近似运算，旨在找到多维数据在某个超完备字典（dictionary） $D$ 上映射的“最佳匹配”。其基本的概念就是要用来自 $D$ 的函数组 $g_{\gamma_n}$ （称为基元，或atom）的加权和来表示希尔伯特空间 $H$ 上的信号 $f$ ：

$f(t) = \sum_{n=0}^{+\infty} a_n g_{\gamma_n}(t)$

其中 $n$ 表示被选取基元的序数， $a_n$ 是每个基元的加权常数。对于固定的字典，匹配追踪会先找到与信号间内积最大的一个基元，再减去该基元带来的影响，然后重复找寻影响力次大的基元直到信号被较好地分解。

相较而言，以傅里叶级数表示的信号来说，字典是构建于正弦基函数之上的。信号处理领域中傅里叶分析的主要缺点就在于它只能提取出信号中常存的特征，而不能适应当前的分析目标信号 $f$ 。

若采用一组极端保险、带有大量冗余的字典，我们就能够找到可以完美匹配信号的 $f$ 函数组。在对信号进行编码与压缩时，最好是能够找到一组映射，使加权和中的大部分系数都接近零（具有“稀疏性”）。

应用

压缩感知与包括欠定系统、群验、稀疏编码、复用、稀疏采样等。在成像科技领域，亦有许多技术如（编码孔与计算摄影学）与压缩感知相关。亦有许多在不同技术完成度下将压缩感知实现的案例。

摄影学

压缩感知技术被用于手机摄像头传感器设计中。这一技术使得在获取图像时所耗费的能量大大降低，可达原先耗费的15分之一——当然，需要引入复杂的解压算法；这一运算可能会需要脱机状态下的预先安装、设置。

压缩感知亦被用于实现单像素摄影。贝尔实验室运用了这一技术，用无镜片单像素相机在栅格中随机选取的孔隙处拍照，以达到成像效果。随着拍照次数的逐渐增多，照片质量也会逐步提高；一般来说，这种技术较之传统的摄影成像技术仅仅需要一小部分的数据占用量，且能完全避免与镜片或聚焦相关的故障或失常；参见[4]
。

全息成像

压缩感知可被用于增加通过单幅全息图中所能得到的立体像素的数量改进全息摄影技术中的图像重建问题。在光学全息图或毫米波全息图采样率不足的情况下，这一技术也能够被用于图像检索以作出改善。

面部识别

压缩感知目前被用于面部识别应用之中，参加Engineers Test Highly Accurate Face Recognition。

核磁共振成像

压缩感知被用于缩短核磁共振成像中的扫描时间，参加[5] 、[6]
与[7]；其中涉及的重建方法包括ISTA、FISTA、SISTA等。

网络诊断

压缩感知在被用于旨在利于网络管理的网络诊断应用中时带来了极佳成效。对网络延时的估计和网络拥塞的探知均可被归纳、建模为非定性的线性方程组系统，其中的参数矩阵正是所分析网络的路由选择矩阵。此外，在互联网情景中，网络路由矩阵常常能够满足压缩感知技术所要求的几个基本要素：低相关性、稀疏性及（可能的）R.I.P条件，请参见[8]
。

短红外摄影

目前，基于压缩感知技术的商用短红外相机已被推出[9] 。这些相机的光敏度大约从0.9µm到1.7µm，在上述波段上，人类的肉眼是无效的。

參考資料

Candès, E.J., & Wakin, M.B., An Introduction To Compressive Sampling, IEEE Signal Processing Magazine, V.21, March 2008

外部链接

"The Fundamentals of Compressive Sensing"

Part 1,
Part 2 and
Part 3: video tutorial by Mark Davenport, Georgia Tech. at
SigView, the IEEE Signal Processing Society Tutorial Library.
Using Math to Turn Lo-Res Datasets Into Hi-Res Samples Wired Magazine article
Compressive Sensing Resources at

Rice University.
Compressed Sensing Makes Every Pixel Count – article in the AMS
What's Happening in the Mathematical Sciences series
Wiki on sparse reconstruction

【上篇】压缩感知的几位鼻祖
【下篇】第一类边界条件，三角单元剖分，线性插值的位场延拓，LDLT高效求解

作者: mandated

该日志由 mandated 于5年前发表在综合分类下，最后更新于 2019年03月16日.
转载请注明: 压缩感知（Compressed sensing）from wiki | 学步园 +复制链接

抱歉!评论已关闭.

学步园