学步园

数学最优化中，由George
Dantzig发明的单纯形法（simplex algorithm）是线性规划问题的数值求解的流行技术。有一个算法与此无关，但名称类似，它是Nelder-Mead法或称下山单纯形法，由Nelder和Mead发现（1965年），这是用于优化多维无约束问题的一种数值方法，属于更一般的搜索算法的类别。

这二者都使用了单纯形的概念，它是N维中的N +
1个顶点的凸包，是一个多胞体：直线上的一个线段，平面上的一个三角形，三维空间中的一个四面体，等等。

1. 标准形式

以下为线性规划的标准形式，假设有n个变量和m个约束。

所有其他形式的线性规划方程组都可以按照下列方式转化成标准形式：

• 目标函数并非最大化：将所有取负。
• 约束条件中存在大于或等于约束：将约束两边取负。
• 约束条件中存在等式：将其转化为两个不等式（一个大于等于，一个小于等于）
• 有的变量没有非负约束：加入新变量，并用替换原来的变量

2. 松弛形式

可以将标准形式的线性规划转化为松弛形式，以方便运算。在原来n个变量，m个约束的线型规划中，加入m个新的变量，将原来的不等式化为等式：

当然，此时依然成立。

我们将这些变量称为非基变量，它们构成的集合记为B。将  这些变量称为基变量，它们构成的集合记为N。简单地理解，基变量能够由非基变量唯一确定。

在这样的定义下，线性规划的松弛形式可以写为如下形式：

因此，线性规划的松弛形式可以由v, c, A, b, N, B唯一确定，其中v是实数，c和b是长度为n+m的向量，A是(n+m)*(n+m)的矩阵。N,
B是整数集合，分别表示非基变量集合以及基变量集合。

3. 转轴操作

转轴操作是单纯形法中的核心操作，其作用是将一个基变量与一个非基变量进行互换。可以将转轴操作理解为从单纯形上的一个顶点走向另一个顶点。

设变量属于B（基变量），变量属于N（非基变量），执行转轴操作pivot(d,e)之后，将变为非基变量，相应地将变为基变量。

具体地说，一开始我们有

移项，得

如果，我们有

将此式代入其他的约束等式以及目标函数，我们就实现了与在基变量和非基变量上的互换。

4. 最优化过程

如果b向量所有元素非负，则显然我们只需要令所有的变量等于0，就可以得到一个可行解。在这种情况下，通过下述最优化过程，我们可以得到该线性规划的最优解，或者指出该线性规划的最优解为无穷大（不存在）。

1. 任取一个非基变量，使得。
2. 选取一个基变量，使得，且最小化
3. 执行转轴操作pivot(d, e)，并转到第一步继续算法。

根据的最小性不难证明pivot(d,
e)不会破坏b的非负性。因此将所有变量取0值仍然是可行解。同时，根据，我们发现v一定是不降的。这就达到了更新解的目的。

不难发现，算法终止有两种情况：

1. 对于所有的非基变量，c均非正。
2. 对于某一个e，所有的均非正。

可以证明，对于第一种情况，我们已经得到了该线性规划的最优解。当前的v即为答案。严格证明比较复杂，但是直观上是很容易理解的。因为所有的非基变量都是非负的，而所有的c都是非正的，因此只要某个非基变量不为0，就会使得目标函数更小。

对于第二种情况来说，很容易证明此时线性规划的最优解是无穷大。只要让其他所有变量均为0，变量为正无穷。由于所有的都非正，因此非基变量的非负性得到保证。同时由于，目标函数值为正无穷。

5. 初始化过程

如果b向量并不全为非负，则我们需要通过初始化过程来找到一个可行解，然后才可以使用最优化过程进行优化。当然，此时原线性规划不一定存在可行解。

具体的方法是，加入一个新的非基变量，并在原线性规划的基础上构造一个新的辅助的线性规划。

注意这里N集合并不包含。

然后，选择一个基变量使得最小，执行转轴操作pivot(d,
0)。不难证明该操作过后所有的b值全部非负。然后，使用前文中所述的最优化过程求解该辅助线性规划。

由于非负，因此该线性规划的答案非正。如果答案为负数，则说明原线性规划不可能让所有的基变量都非负，因此原线性规划无可行解。否则，只要令所有变量为0，并去掉变量，就可以得到可行解。

在从辅助线性规划转化到原来的线性规划的过程中，如果已经是非基变量，则可以将其从约束条件和目标函数中直接去掉。否则，需要任取一个非基变量执行pivot(0,
e)，将变为非基变量。由于此时是基变量且，故一定成立，因此这个转轴操作不会破坏b向量的非负性。

6. 效率分析

在采用Blind's法则选择用于转轴操作的d和e（相同值的情况下取字典序最小）之后，可以证明单纯形法一定能够在有限步之后终止，但是最坏情况算法的时间复杂度为指数级别的，而且可以构造出让单纯形法的时间复杂度达到指数级别的具体实例。不过实践证明在绝大多数情况下单纯形法的效率非常令人满意。

单纯形法的最坏时间复杂度为指数级别，并不意味着线性规划不存在多项式级别的算法。椭球算法和内点算法均为解决线性规划的多项式时间算法。

7. 参考

• Greenberg, Harvey J., Klee-Minty Polytope Shows Exponential Time Complexity of Simplex Method University
  of Colorado at Denver (1997) PDF
  download
• Frederick S. Hillier and Gerald J. Lieberman: Introduction to Operations Research, 8th edition.
  McGraw-Hill. ISBN
  0-07-123828-X
• Thomas
  H. Cormen, Charles
  E. Leiserson, Ronald
  L. Rivest, and Clifford
  Stein.Introduction to Algorithms, Second Edition. MIT Press and McGraw-Hill, 2001.ISBN
  0-262-03293-7. Section 29.3: The simplex algorithm, pp.790-804.
• IOI2007国家集训队论文，《浅谈信息学竞赛中的线性规划——简洁高效的单纯形法实现与应用》，作者：李宇骞

8. 参看

• Nelder-Mead方法
• 求解单纯形法问题的方法

9. 外部连接

• 线性规划和单纯形法简介 作者Spyros
  Reveliotis（乔治亚理工）。
  • 分步单纯形法求解器 可以求解线性规划问题。
• 基于Java的交互式单纯形工具 由Argonne国家实验室提供。
• 单纯形法 作者Elmer
  G. Wiens。演示算法细节，使用了单纯形表。
• 单纯形法教程 作者Stefan
  Waner，hofstra.edu。
• 单纯形法分解 Mazoo学习网志

http://wapedia.mobi/zh/单纯形法

 

 

单纯形法

　　可按现代电子计算机标准程序求解线性规划模型的一般方法。分为代数形式的单纯形法和表格形式的单纯形法。前者提供基本算法所依据的逻辑规则，适用于在电子计算机上进行求解运算；后者将变量和数据列成表格，适用于笔算。两者在数学上是等价的。单纯形法是由美国数学家G.B.丹齐克（1914～　）于1947年提出来的，它与苏联数学家Л.Β.坎托罗维奇（1912～　）于1938年提出的解乘数法相类似。
　　根据单纯形法的原理，在线性规划问题中，决策变量（控制变量）x₁，x₂，…x _n的值称为一个解,满足所有的约束条件的解称为可行解。使目标函数达到最大值（或最小值）的可行解称为最优解。这样，一个最优解能在整个由约束条件所确定的可行区域内使目标函数达到最大值（或最小值）。求解线性规划问题的目的就是要找出最优解。
　　可能出现下列情况之一：①存在着一个最优解；②存在着无穷多个最优解；③不存在最优解，这只在两种情况下发生，即没有可行解或各项约束条件不阻止目标函数的值无限增大（或向负的方向无限增大）。
　　要缩小对最优解的搜索范围，就必须认识最优解的一般性质，最优解如果存在的话，则它必然处于可行区域的边界上。
　　任何一项约束条件的边界方程是用“＝”号来替换该约束条件中的“≤”或“≥”号而得到的。每一个边界方程确定一个超平面。因此，可行区域的边界是由那些满足一个或同时满足几个边界方程（即处在作为边界的一个或几个超平面上）的可行解所组成，而且最优解必在其中。最优解不仅是在可行区域的边界上，而且也在这个区域的一个隅角上。一个可行解，如果不处在由另两个可行解连接起来的任何线段上，它就是一个角点可行解。如果连接两个角点可行解的线段处在可行区域的边界上，这两个角点可行解就称为相邻的角点可行解。角点可行解具有下列三个重要性质：①如果存在着一个最优解，那么它必定是角点可行解。如果存在有多个最优解，那么至少有两个最优解必定是相邻的角点可行解。②只存在有限个数的角点可行解。③如果一个角点可行解按目标函数值来衡量时比其所有的相邻角点可行解更好一些，那它就比所有其他角点可行解都更好，也就是最优解。
　　上述这些性质构成单纯形法的原理基础。最后一个性质的重要性在于它为一个角点可行解是否是最优解提供了一种简便的检验标准，因而毋需列举所有的可行解。单纯形法正是利用了这个性质，只要检查少数的角点可行解，并且一旦这个最优性检验获得通过就可立即停止运算。
　　单纯形法的运算步骤可归结为：①起始步骤──在一个角点可行解上开始。②迭代步骤──移动至一个更好一些的相邻角点可行解（根据需要反复进行这一步骤）。③停止法则──在当前角点可行解比所有相邻角点可行解都更好些时停止。当前角点可行解就是一个最优解。
　　单纯形法的优点及其成功之处在于它只需要较少的有限次数的迭代，即可找到最优解。

 

 

单纯形法的提出及依据

　　单纯形法是美国数学家George Dantzig于1947年首先提出的。

　　其理论根据是：线性规划问题的可行域是n维向量空间Rⁿ中的多面凸集，其最优值如果存在必在该凸集的某顶点处达到，该顶点所对应的可行解称为基本可行解。

单纯形法的基本思想

　　单纯形法是一种多变量函数的寻优方法，其主要思想是先找一个基本可行解，判断是否为最优解，如果不是则找另外一个解，再进行判定，如此迭代运算，直至找到最优解或者判定其无界。

单纯形法的特点

　　单纯形法是一种直接、快速的搜索最小值方法，其优点是对目标函数的解析性没有要求，收敛速度快，适用面较广。

　　单纯形法的一般解题步骤可归纳如下：

　　1.把线性规划问题的约束方程组表达成典范型方程组，找出基本可行解作为初始基本可行解。

　　2.若基本可行解不存在，即约束条件有矛盾，则问题无解。

　　3.若基本可行解存在，从初始基本可行解作为起点，根据最优性条件和可行性条件，引入非基变量取代某一基变量，找出目标函数值更优的另一基本可行解。

　　4.按步骤3进行迭代,直到对应检验数满足最优性条件（这时目标函数值不能再改善），即得到问题的最优解。

　　5.若迭代过程中发现问题的目标函数值无界，则终止迭代。

改进的单纯形法

　　原单纯形法不是很经济的算法。1953年美国数学家G.B.丹齐克为了改进单纯形法每次迭代中积累起来的进位误差，提出改进单纯形法。其基本步骤和单纯形法大致相同，主要区别是在逐次迭代中不再以高斯消去法为基础，而是由旧基阵的逆去直接计算新基阵的逆，再由此确定检验数。这样做可以减少迭代中的累积误差，提高计算精度，同时也减少了在计算机上的存储量。

　　改进的单纯形法是在单纯形操作中引入变异操作，以此来增强全局搜索能力。具体做法是：

　　首先，进行基本单纯形法操作，快速得到局部极小值，再对极小值点在取值范围内进行变异操作，并重新进行基本单纯形法操作，直到得到最优解为止。该算法的计算步骤如下：

　　(1)选取初始单纯形，初始步长L，最大变异次数mmax，计数器m=0；

　　(2)进行基本单纯形操作，找到一个极值点X₁；

　　(3)以极值点置作新的顶点，再选取初始单纯形，并进行新一轮的单纯形操作，得到新的极值点，两极值点对应的目标函数为R₁,R₂；

　　(4)若R₁ > R₂,R₁ = R₂,X₁ = X₂,

　　代入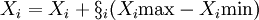：　　(i=1,2,…,t)(1)

式中，X_imax、X_imin为参数X_i的上、下限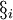；为0到1之间的随机数。

　　(5)若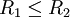，对进行变异操作，计数器m=m+1：

　　(6)若计数器m < mmax，转(1)，否则输出结果X₁。

参考文献

 

 

在数学 最优化理论 单纯形算法由创造 美国 数学家 乔治Dantzig 在 1947是普遍 算法 为 数字 解答 线性规划 问题。
学报 计算在科学和设计 列出它作为世纪的名列前茅10种算法之一。^[1]

一个无关，但相似地名为方法是 Nelder-Mead方法 或 下坡单纯形法 归结于Nelder
& Mead (1965)和a 数字方法 为优选许多尺寸 跌宕的问题，属于更加一般的类 搜索算法.

在两种情况下，方法使用a的概念 单缸是a polytope N +
1端点 N 维度： a 线段 在一个维度，
a 三角 在二个维度，
a 四面体 在三维空间等等。

 

描述

 

 

一个线性规划问题包括收藏品 线性 不平等在一定数量 真正 可变物 并且指定的 线性函数 (在这些实变量)将最大化或减到最小。进一步细节在提供 线性规划 文章。

用几何学术语我们考虑a 闭合 凸面 polytope, P通过相交定义一定数量 半空格 在 n-尺寸 欧几里德的空间;
每半空格是在a的一边说谎的区域 超平面.
如果宗旨将最大化一线性功能 L(x)，考虑超平面 H(c)定义 L(x) = c; c 增量，这些形成一个平行的家庭。 如果问题很好被摆在，我们想要发现最大的价值 c 这样 H(c)相交 P (如果没有这样最大的价值 c照原样)，这不是一个合理的问题为优化。
我们可以在这种情况下显示那优值 c 在界限被获得 P. 方法为在P工作发现这个最优点用几个方式： 某一企图经过移动改进可能的点通过内部 P (所谓 内部点方法);
其他在搜寻最宜的界限开始并且保持。

单纯形算法跟随这后者方法学。想法是沿小平面移动 P 寻找最宜，从点对点。 注意，除非最宜在是平行的边缘或面孔发生 H最宜将是独特的并且发生在polytope的端点。
如果最宜在是平行的边缘或面孔被找到 H 然后最宜不是独特的，并且可以获得在任何点在边缘或面孔。因为单纯形算法与发现优选的点仅有关(即使其他相等优选的点存在)，单一地注视着避开a的边缘移动是可能的 单缸忽略内部。算法指定怎么这将做。

我们以polytope的某一端点开始，并且在每叠代我们选择一个毗邻端点这样目标函数的价值不减少。如果这样端点不存在，我们发现了一种解答到问题。但通常，这样一个毗邻端点是非独特和a 枢轴规则 必须指定确定采摘的哪个端点。各种各样的枢轴规则存在。

在 1972Klee和有薄荷味 ^[2] 一个线性规划问题的举例子 polytope P 是畸变 n-尺寸立方体。
他们表示，单纯形法如由Dantzig公式化参观全部2ⁿ 端点在到达在优选的端点之前。 这表示，算法的最坏的复杂是 指数时间.
相似的例子为其他枢轴规则被找到了。如果有一个枢轴规则与，它是一个未解决的问题 多项时间 最坏的复杂。

然而，单纯形法实践上是卓越地高效率的。企图解释此使用平均复杂或(最近)使光滑的复杂的概念。

其他算法为解决线性规划问题在被描述 线性规划 文章。

问题输入

考虑一个线性规划问题，

最大化

受支配

单纯形算法要求线性规划问题 被增添的形式.
问题可能然后被写如下以矩阵形式：

最大化 Z 在：

那里 x 是可变物从 标准格式, x_s 是被介绍的松弛变数从增广过程， c 包含优化系数， A 并且 b 描述约束方程系统，和 Z 是将最大化的可变物。

系统典型地是 underdetermined，因为可变物的数量超出等式的数量。 在可变物的数量和等式之间的数量的区别给我们 自由程度 与问题相关。因此所有解答，优选或者没有，将包括任意价值的一定数量的可变物。单纯形算法使用零作为这任意价值，并且可变物的数量以价值零合计自由程度。

非零值的可变物叫 基变量和零的价值的可变物叫 nonbasic可变物 在单纯形算法。 [这个定义是疑难的，因为基变量可能也采取零的价值。]

这个形式简化发现最初 基本的可行的解答 (BF)，从所有可变物从 标准格式 可以被选择nonbasic (零)，而在介绍的所有新的可变物 被增添的形式 是基本的(非零)，因为他们的价值可以琐细地被计算(
为他们，因为被增添的问题矩阵是对角的在它的右中卫)。

修改过的单纯形算法

单纯形算法的矩阵形式

在单纯形算法的所有叠代，场面将是这个形式：

那里是基变量系数在 c-矩阵; 并且 B 是专栏 对应于基变量。

它值得注意那 B 并且 是唯一的可变物在这个等式(除了 Z 并且 x 当然)。一切是恒定的在算法中。

算法

• 选择a 基本的可行的解答 (BF)如所示上述

这暗示那 B 是单位矩阵，和 是零传染媒介。

• 当nonoptimal解答时：
  • 确定最高的梯度的方向

  选择可变物与系数相关 那有最高 消极 巨大。 这nonbasic可变物，我们称 进入基本将增加到帮助最大化问题。

  • 确定最大步长

  使用确定哪个的subequation基变量首先到达零，当 进入基本 增加。 这可变物，我们称留给基本 然后变得nonbasic。因为现有的基本可变物在场面，发生对角地这操作只介入唯一分裂为每个基变量。

  • 重写问题

  修改 B 并且 占新的基变量。 这将自动地做场面对角线为现有和新的基变量。

  • 检查改善

  重覆做法，直到进一步改善不是可能的，意味所有系数是正面的。做法也被终止，如果所有系数是零，并且算法在圈子走了并且再访了一个早先状态。

修改单纯形法的共同的实施

• Bartels-Golub方法
• 稀稀落落的Bartels-Golub方法
• Forrest-Tomlin方法
• Reid的方法

参考

• 格林柏格， Harvey J.， Klee有薄荷味的Polytope显示单纯形法的指数时间复杂 科罗拉多大学在丹佛(1997) PDF下载
• Frederick S。更加多小山和杰拉尔德J。 Lieberman ： 运筹学介绍第8编辑。 McGraw小山。 国际标准书号0-07-123828-X
• 托马斯H。
  Cormen, 查尔斯E。
  Leiserson, 罗纳德L。
  Rivest和 Clifford斯坦. 算法介绍再版。
  MIT新闻和McGraw小山2001年。 国际标准书号0-262-03293-7.
  第29.3部分： 单纯形算法， pp.790-804。
• Hamdy A。 Taha ： 运筹学： 介绍第8编辑。，学徒霍尔2007年。 国际标准书号0-13-188923-0
• 理查B。 Darst ： 线性规划介绍： 应用和引伸

1. ^ 计算在科学和设计容量2，没有。
   1, 2000
2. ^ 格林柏格，援引：
   v. Klee和G.J。 有薄荷味。 “多么好是单纯形算法？” 在O。 Shisha，编辑， 不平等， III页159-175。 学术出版社，纽约， NY 1972年