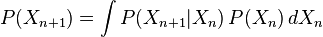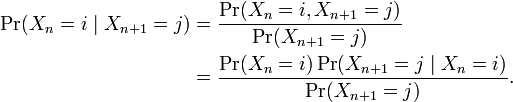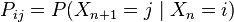马尔可夫

现在的位置: 首页 > 综合 > 正文

2019年05月04日 ⁄ 综合 ⁄ 共 4648字 ⁄ 字号小中大 ⁄ 评论关闭

马尔可夫性质是概率论中的一个概念。当一个随机过程在给定现在状态及所有过去状态情况下，其未来状态的条件概率分布仅依赖于当前状态；换句话说，在给定现在状态时，它与过去状态（即该过程的历史路径）是条件独立的，那么此随机过程即具有马尔可夫性质。具有马尔可夫性质的过程通常称之为马尔可夫过程。

数学上，如果 $X (t), t > 0$ 为一个随机过程，则马尔可夫性质就是指

$/mathrm{Pr}/big[X(t+h) = y /,|/, X(s) = x(s), s /leq t/big] = /mathrm{Pr}/big[X(t+h) = y /,|/, X(t) = x(t)/big], /quad /forall h > 0.$

马尔可夫过程通常称其为（时间）齐次，如果满足

$/mathrm{Pr}/big[X(t+h) = y /,|/, X(t) = x(t)/big] = /mathrm{Pr}/big[X(h) = y /,|/, X(0) = x(0)/big], /quad /forall t, h > 0,$

除此之外则被称为是（时间）非齐次的。齐次马尔可夫过程通常比非齐次的来得简单，构成了最重要的一类马尔可夫过程。

某些情况下，明显的非马尔可夫过程也可以通过扩展“现在”和“未来”状态的概念来构造一个马尔可夫表示。设 $X$ 为一个非马尔可夫过程。我们就可以定义一个新的过程 $Y$ ，使得每一个 $Y$ 的状态表示 $X$ 的一个时间区间上的状态，用数学方法来表示，即，

$Y(t) = /big/{ X(s) : s /in [a(t), b(t)] /, /big/}.$

如果 $Y$ 具有马尔可夫性质，则它就是 $X$ 的一个马尔可夫表示。在这个情况下， $X$ 也可以被称为是二阶马尔可夫过程。更高阶马尔可夫过程也可类似地来定义。

具有马尔可夫表示的非马尔可夫过程的例子，例如有移动平均时间序列。

最有名的马尔可夫过程为马尔可夫链，但不少其他的过程，包括布朗运动也是马尔可夫过程。

隐马尔可夫模型（Hidden Markov Model，HMM）是统计模型，它用来描述一个含有隐含未知参数的马尔可夫过程。其难点是从可观察的参数中确定该过程的隐含参数。然后利用这些参数来作进一步的分析，例如模式识别。

在正常的马尔可夫模型中，状态对于观察者来说是直接可见的。这样状态的转换概率便是全部的参数。而在隐马尔可夫模型中,状态并不是直接可见的，但受状态影响的某些变量则是可见的。每一个状态在可能输出的符号上都有一概率分布。因此输出符号的序列能够透露出状态序列的一些信息。

[编辑]马尔可夫模型的演化

上边的图示强调了HMM的状态变迁。有时，明确的表示出模型的演化也是有用的,我们用x（t₁）与x（t₂）来表达不同时刻t₁ 和t₂的状态。

Temporal evolution of a hidden Markov model

在这个图中,每一个时间块（x(t), y(t)）都可以向前或向后延伸。通常，时间的起点被设置为t=0 或 t=1.

[编辑]使用隐马尔可夫模型

HMM有三个典型(canonical)问题:

已知模型参数，计算某一特定输出序列的概率.通常使用forward算法解决.
已知模型参数，寻找最可能的能产生某一特定输出序列的隐含状态的序列.通常使用Viterbi算法解决.
已知输出序列，寻找最可能的状态转移以及输出概率.通常使用Baum-Welch算法以及Reversed Viterbi算法解决.

另外,最近的一些方法使用Junction tree算法来解决这三个问题。

[编辑]具体实例

假设你有一个住得很远的朋友,他每天跟你打电话告诉你他那天做了什么.你的朋友仅仅对三种活动感兴趣:公园散步,购物以及清理房间.他选择做什么事情只凭天气.你对于他所住的地方的天气情况并不了解,但是你知道总的趋势.在他告诉你每天所做的事情基础上,你想要猜测他所在地的天气情况.

你认为天气的运行就像一个马尔可夫链.其有两个状态 "雨"和"晴",但是你无法直接观察它们,也就是说,它们对于你是隐藏的.每天,你的朋友有一定的概率进行下列活动:"散步", "购物", 或 "清理". 因为你朋友告诉你他的活动,所以这些活动就是你的观察数据.这整个系统就是一个隐马尔可夫模型HMM.

你知道这个地区的总的天气趋势,并且平时知道你朋友会做的事情.也就是说这个隐马尔可夫模型的参数是已知的.你可以用程序语言(Python)写下来:

states = ('Rainy', 'Sunny')

observations = ('walk', 'shop', 'clean')

start_probability = {'Rainy': 0.6, 'Sunny': 0.4}

transition_probability = {
   'Rainy' : {'Rainy': 0.7, 'Sunny': 0.3},
   'Sunny' : {'Rainy': 0.4, 'Sunny': 0.6},
   }

emission_probability = {
   'Rainy' : {'walk': 0.1, 'shop': 0.4, 'clean': 0.5},
   'Sunny' : {'walk': 0.6, 'shop': 0.3, 'clean': 0.1},
   }

在这些代码中,start_probability代表了你对于你朋友第一次给你打电话时的天气情况的不确定性(你知道的只是那个地方平均起来下雨多些).在这里,这个特定的概率分布并非平衡的,平衡概率应该接近（在给定变迁概率的情况下）{'Rainy': 0.571, 'Sunny': 0.429}< transition_probability 表示基于马尔可夫链模型的天气变迁,在这个例子中,如果今天下雨,那么明天天晴的概率只有30%.代码emission_probability 表示了你朋友每天做某件事的概率.如果下雨,有 50% 的概率他在清理房间;如果天晴,则有60%的概率他在外头散步.

这个例子在Viterbi算法页上有更多的解释。

[编辑]隐马尔可夫模型的应用

语音识别、中文断词/分词或光学字符识别
机器翻译
生物信息学和基因组学
- 基因组序列中蛋白质编码区域的预测
- 对于相互关联的DNA或蛋白质族的建模
- 从基本结构中预测第二结构元素
还有更多...

马尔可夫链，因俄罗斯数学家安德烈·马尔可夫得名，是数学中具有马尔可夫性质的离散时间随机过程。该过程中，在给定当前知识或信息的情况下，只有当前的状态用来预测将来，过去（即当前以前的历史状态）对于预测将来（即当前以后的未来状态）是无关的。

在马尔可夫链的每一步，系统根据概率分布，可以从一个状态变到另一个状态,也可以保持当前状态。状态的改变叫做过渡，与不同的状态改变相关的概率叫做过渡概率。随机漫步就是马尔可夫链的例子。随机漫步中每一步的状态是在图形中的点，每一步可以移动到任何一个相邻的点，在这里移动到每一个点的概率都是相同的(无论之前漫步路径是如何的)。

历史

马尔可夫在1906年首先做出了这类过程。而将此一般化到可数无限状态空间是由柯尔莫果洛夫在1936年给出的。马尔可夫链与布朗运动以及遍历假说这两个二十世纪初期物理学重要课题是相联系的，但马尔可夫寻求的似乎不仅于数学动机，名义上是对于纵属事件大数法则的扩张。

定义

马尔可夫链是随机变量 $X 1, X 2, X 3 ...$ 的一个数列。这些变量的范围，即他们所有可能取值的集合，被称为“状态空间”，而 $X n$ 的值则是在时间 $n$ 的状态。如果 $X n + 1$ 对于过去状态的条件概率分布仅是 $X n$ 的一个函数，则

$P(X_{n+1}=x|X_0, X_1, X_2, /ldots, X_n) = P(X_{n+1}=x|X_n). /,$

这里 $x$ 为过程中的某个状态。上面这个恒等式可以被看作是马尔可夫性质。

性质

可还原性

马尔可夫链是由一个条件分布来表示的

$P(X_{n+1}| X_n)/,$

这被称为是随机过程中的“转移概率”。这有时也被称作是“一步转移概率”。二、三，以及更多步的转移概率可以导自一步转移概率和马尔可夫性质：

$P(X_{n+2}|X_n) = /int P(X_{n+2},X_{n+1}|X_n)/,dX_{n+1} = /int P(X_{n+2}|X_{n+1}) /, P(X_{n+1}|X_n) /, dX_{n+1}$

同样，

$P(X_{n+3}|X_n) = /int P(X_{n+3}|X_{n+2}) /int P(X_{n+2}|X_{n+1}) /, P(X_{n+1}|X_n) /, dX_{n+1} /, dX_{n+2}$

这些式子可以通过乘以转移概率并求 $k - 1$ 次积分来一般化到任意的将来时间 $n + k$ 。

周期性

边际分布 $P (X n)$ 是在时间为 $n$ 时的状态的分布。初始分布为 $P (X 0)$ 。该过程的变化可以用以下的一个时间步幅来描述：

$P(X_{n+1}) = /int P(X_{n+1}|X_n)/,P(X_n)/,dX_n$

这是Frobenius-Perron equation的一个版本。这时可能存在一个或多个状态分布 $π$ 满足

$/pi(X) = /int P(X|Y)/,/pi(Y)/,dY$

其中 $Y$ 只是为了便于对变量积分的一个名义。这样的分布 $π$ 被称作是“平稳分布”（Stationary Distribution）或者“稳态分布”（Steady-state Distribution）。一个平稳分布是一个对应于特征值为 $1$ 的条件分布函数的特征方程。

平稳分布是否存在，以及如果存在是否唯一，这是由过程的特定性质决定的。“不可约”是指每一个状态都可来自任意的其它状态。当存在至少一个状态经过一个固定的时间段后连续返回，则这个过程被称为是“周期的”。

重现性

各态历遍性

律动性

平稳状态分析和极限分布

可反转马尔可夫链

可反转马尔可夫链类似于应用贝叶斯定理来反转一个条件概率:

$/begin{align} /Pr(X_{n}=i/mid X_{n+1}=j) & = /frac{/Pr(X_n = i, X_{n+1} = j)}{/Pr(X_{n+1} = j)} // & = /frac{/Pr(X_{n} = i)/Pr(X_{n+1} = j/mid X_n=i)}{/Pr(X_{n+1} = j)}. /end{align}$

以上就是反转的马尔可夫链。因而，如果存在一个π，使得:

$/pi_i p_{ij} = /pi_j p_{ji}./,$

那么这个马尔可夫链就是可反转的。

这个条件也被称为细致平衡 (detailed balance)条件。

对于所有的i求和:

$/sum_i /pi_i p_{ij} = /pi_j/,$

所以，对于可反转马尔可夫链，π总是一个平稳分布。

有限状态空间中的马尔可夫链

如果状态空间是有限的，则转移概率分布可以表示为一个具有 $(i, j)$ 元素的矩阵，称之为“转移矩阵”：

$P_{ij} = P(X_{n+1}=j/mid X_n=i) /,$

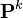对于一个离散状态空间， $k$ 步转移概率的积分即为求和，可以对转移矩阵求 $k$ 次幂来求得。就是说，如果 $/mathbf{P}$ 是一步转移矩阵， $/mathbf{P}^k$ 就是 $k$ 步转移后的转移矩阵。

平稳分布是一个满足以下方程的矢量

$/mathbf{P}/pi^* = /pi^*$ .

在此情况下，稳态分布 $π *$ 是一个对应于特征根为 $1$ 的、该转移矩阵的特征矢量。

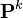如果转移矩阵 $/mathbf{P}$ 不可约，并且是非周期的，则 $/mathbf{P}^k$ 收敛到一个每一列都是不同的平稳分布 $π *$ ，并且，

$/lim_{k/rightarrow/infty}/mathbf{P}^k/pi=/pi^*$ ,

独立于初始分布 $π$ 。这是由Perron-Frobenius theorem所指出的。

正的转移矩阵（即矩阵的每一个元素都是正的）是不可约和非周期的。矩阵被称为是一个随机矩阵，当且仅当这是某个马尔可夫链中转移概率的矩阵。

注意：在上面的定式化中，元素 $(i, j)$ 是由j转移到i的概率。有时候一个由元素 $(i, j)$ 给出的等价的定式化等于由i转移到j的概率。在此情况下，转移矩阵仅是这里所给出的转移矩阵的转置。另外，一个系统的平稳分布是由该转移矩阵的左特征矢量给出的，而不是右特征矢量。

转移概率独立于过去的特殊况为熟知的Bernoulli scheme。仅有两个可能状态的Bernoulli scheme被熟知为伯努利过程

科学应用

统计

马尔可夫链通常用来建模排队理论和统计学中的建模，还可作为信号模型用于熵编码技术，如算术编码（著名的LZMA数据压缩算法就使用了马尔可夫链与类似于算术编码的区间编码）。

生物

马尔可夫链也有众多的生物学应用，特别是人口过程，可以帮助模拟生物人口过程的建模。隐蔽马尔可夫模型还被用于生物信息学，用以编码区域或基因预测。

地理

马尔可夫链最近的应用是在地理统计学（geostatistics）中。其中，马尔可夫链用在基于观察数据的二到三维离散变量的随机模拟。这一应用类似于“克里金”地理统计学（Kriging geostatistics），被称为是“马尔可夫链地理统计学”。这一马尔可夫链地理统计学方法仍在发展过程中。

因特网应用

谷歌所使用的网页排序算法（PageRank）就是由马尔可夫链定义的。马尔可夫模型也被应用于分析用户浏览网页的行为。一阶或者二阶的马尔可夫模型可以用于对一个用户从某一网络链接转移到另一链接的行为进行建模，然后这些模型可以用于对用户之后的浏览行为进行预测。

马尔可夫模仿文本生成器

马尔可夫过程，能为给定样品文本，生成粗略，但看似真实的文本：他们被用于众多供消遣的“模仿生成器”软件。马尔可夫链还被用于谱曲。

【上篇】传统与现代的邂逅——新中式景观设计
【下篇】应力模型

作者: ecos

该日志由 ecos 于5年前发表在综合分类下，最后更新于 2019年05月04日.
转载请注明: 马尔可夫 | 学步园 +复制链接

抱歉!评论已关闭.

学步园