现在的位置: 首页 > 综合 > 正文

高斯混合模型

2019年11月10日 ⁄ 综合 ⁄ 共 10081字 ⁄ 字号 小 中 大 ⁄ 评论关闭
文章目录

本文就高斯混合模型（GMM,Gaussian Mixture Model）参数如何确立这个问题，详细讲解期望最大化（EM,Expectation Maximization）算法的实施过程。

0 预备知识

l  设离散型随机变量X的分布律为

则称 为X的数学期望或均值

l  设连续型随机变量X的概率密度函数（PDF）为

其数学期望定义为

l  称为随机变量X的方差，称为X的标准差

l  正态分布 ~

概率密度函数

l  设（X, Y）为二维随机变量，若存在，则称其为随机变量X和Y的协方差，记为

l  多维高斯（正态）分布概率密度函数PDF定义如下：

其中，x是维数为n的样本向量（列向量），是期望，是协方差矩阵，表示的行列式，表示的逆矩阵，表示的转置。

1 高斯混合模型概述

1.1.   单高斯模型（Single GaussianModel, SGM）

          （1）

对于单高斯模型，由于可以明确训练样本是否属于该高斯模型（如训练人脸肤色模型时，将人脸图像肤色部分分割出来，形成训练集），故μ通常由训练样本均值代替，由样本方差代替。为了将高斯分布用于模式分类，假设训练样本属于类别K，那么，式(1)可以改为如下形式：

       （2）

式(2)表明样本属于类别K的概率大小。从而将任意测试样本输入式(2)，均可以得到一个标量，然后根据阈值t来确定该样本是否属于该类别，阈值t可以为经验值，也可以通过实验确定。

1.2.   高斯混合模型（GaussianMixture Model，GMM）

高斯混合模型是单一高斯概率率密度函数的延伸。例如：有一批观察数据，数据个数为n，在d 维空间中的分布不是椭球状（如图 1(a)），那么就不适合以一个单一的高斯密度函数来描述这些数据点的概率密度函数。此时我们采用一个变通方案，

假设每个点均由一个单高斯分布生成（如图 1(b)，具体参数，未知），而这一批数据共由M（明确）个单高斯模型生成，具体某个数据属于哪个单高斯模型未知，且每个单高斯模型在混合模型中占的比例未知，将所有来自不同分布的数据点混在一起，该分布称为高斯混合分布。

从数学上讲，我们认为这些数据的概率分布密度函数可以通过加权函数表示：，其中

表示第j个SGM的PDF。

       令，GMM共有M个SGM，现在，我们就需要通过样本集X来估计GMM的所有参数：，样本X的概率公式为：

      

       通常用EM（ExpectationMaximum）算法对GMM参数进行估计。

       算法流程：

       （1）初始化

       方案1：协方差矩阵设为单位矩阵，每个模型比例的先验概率；均值设为随机数。

       方案2：由k均值（k-means）聚类算法对样本进行聚类，利用各类的均值作为，并计算，取各类样本占样本总数的比例。

       （2）估计步骤（E-step）

       令的后验概率为

      

       （3）最大化步骤（M-step）

       更新权值：

       更新均值：

       更新方差矩阵：

       （4）收敛条件

       不断地迭代步骤（2）和（3），重复更新上面三个值，直到，其中为更新参数后计算的值，即前后两次迭代得到的结果变化小于一定程度则终止迭代，通常。

1.3.   K-means算法

k-means算法是输入聚类个数k，以及包含 n个数据对象的数据库，输出满足方差最小标准的k个聚类。同一聚类中的对象相似度较高；而不同聚类中的对象相似度较小。聚类相似度是利用各聚类中对象的均值所获得一个“中心对象”（引力中心）来进行计算的。

k-means算法的基本步骤：

（1）从 n个数据对象任意选择k个对象作为初始聚类中心；

（2）根据每个聚类对象的均值（中心对象），计算每个对象与这些中心对象的距离；并根据最小距离重新对相应对象进行划分；

（3）重新计算每个（有变化）聚类的均值（中心对象）；

（4）计算标准测度函数，当满足一定条件，如函数收敛时，则算法终止；如果条件不满足则回到步骤（2）。

单高斯分布模型GSM

多维变量X服从高斯分布时，它的概率密度函数PDF为：

x是维度为d的列向量，u是模型期望，Σ是模型方差。在实际应用中u通常用样本均值来代替，Σ通常用样本方差来代替。很容易判断一个样x本是否属于类别C。因为每个类别都有自己的u和Σ，把x代入（1）式，当概率大于一定阈值时我们就认为x属于C类。

从几何上讲，单高斯分布模型在二维空间应该近似于椭圆，在三维空间上近似于椭球。遗憾的是在很多分类问题中，属于同一类别的样本点并不满足“椭圆”分布的特性。这就引入了高斯混合模型。

高斯混合模型GMM

GMM认为数据是从几个GSM中生成出来的，即

K需要事先确定好，就像K-means中的K一样。πk是权值因子。其中的任意一个高斯分布N(x;uk,Σk)叫作这个模型的一个component。这里有个问题，为什么我们要假设数据是由若干个高斯分布组合而成的，而不假设是其他分布呢？实际上不管是什么分布，只K取得足够大，这个XX Mixture Model就会变得足够复杂，就可以用来逼近任意连续的概率密度分布。只是因为高斯函数具有良好的计算性能，所GMM被广泛地应用。

GMM是一种聚类算法，每个component就是一个聚类中心。即在只有样本点，不知道样本分类（含有隐含变量）的情况下，计算出模型参数（π，u和Σ）----这显然可以用EM算法来求解。再用训练好的模型去差别样本所属的分类，方法是：step1随机选择K个component中的一个（被选中的概率是πk）；step2把样本代入刚选好的component，判断是否属于这个类别，如果不属于则回到step1。

样本分类已知情况下的GMM

当每个样本所属分类已知时，GMM的参数非常好确定，直接利用Maximum Likelihood。设样本容量为N，属于K个分类的样本数量分别是N1,N2,...,Nk，属于第k个分类的样本集合是L(k)。

样本分类未知情况下的GMM

有N个数据点，服从某种分布Pr(x;θ)，我们想找到一组参数θ，使得生成这些数据点的概率最大，这个概率就是

称为似然函数（Lilelihood Function）。通常单个点的概率很小，连乘之后数据会更小，容易造成浮点数下溢，所以一般取其对数，变成

称为log-likelihood function。

GMM的log-likelihood function就是：

这里每个样本xi所属的类别zk是不知道的。Z是隐含变量。

我们就是要找到最佳的模型参数，使得(6)式所示的期望最大，“期望最大化算法”名字由此而来。

EM法求解

EM要求解的问题一般形式是

Y是隐含变量。

我们已经知道如果数据点的分类标签Y是已知的，那么求解模型参数直接利用Maximum Likelihood就可以了。EM算法的基本思路是：随机初始化一组参数θ(0)，根据后验概率Pr(Y|X;θ)来更新Y的期望E(Y)，然后用E(Y)代替Y求出新的模型参数θ(1)。如此迭代直到θ趋于稳定。

E-Step E就是Expectation的意思，就是假设模型参数已知的情况下求隐含变量Z分别取z1,z2,...的期望，亦即Z分别取z1,z2,...的概率。在GMM中就是求数据点由各个 component生成的概率。

注意到我们在Z的后验概率前面乘以了一个权值因子αk，它表示在训练集中数据点属于类别zk的频率，在GMM中它就是πk。

 M-Step M就是Maximization的意思，就是用最大似然的方法求出模型参数。现在我们认为上一步求出的r(i,k)就是“数据点xi由component k生成的概率”。根据公式(3),(4),(5)可以推出：

与K-means比较

相同点：都是可用于聚类的算法；都需要指定K值。

不同点：GMM可以给出一个样本属于某类的概率是多少。

聚类的方法有很多种，k-means要数最简单的一种聚类方法了，其大致思想就是把数据分为多个堆，每个堆就是一类。每个堆都有一个聚类中心（学习的结果就是获得这k个聚类中心），这个中心就是这个类中所有数据的均值，而这个堆中所有的点到该类的聚类中心都小于到其他类的聚类中心（分类的过程就是将未知数据对这k个聚类中心进行比较的过程，离谁近就是谁）。其实k-means算的上最直观、最方便理解的一种聚类方式了，原则就是把最像的数据分在一起，而“像”这个定义由我们来完成，比如说欧式距离的最小，等等。想对k-means的具体算法过程了解的话，请看这里。而在这篇博文里，我要介绍的是另外一种比较流行的聚类方法----GMM（Gaussian
Mixture Model）。

    GMM和k-means其实是十分相似的，区别仅仅在于对GMM来说，我们引入了概率。说到这里，我想先补充一点东西。统计学习的模型有两种，一种是概率模型，一种是非概率模型。所谓概率模型，就是指我们要学习的模型的形式是P(Y|X)，这样在分类的过程中，我们通过未知数据X可以获得Y取值的一个概率分布，也就是训练后模型得到的输出不是一个具体的值，而是一系列值的概率（对应于分类问题来说，就是对应于各个不同的类的概率），然后我们可以选取概率最大的那个类作为判决对象（算软分类soft
assignment）。而非概率模型，就是指我们学习的模型是一个决策函数Y=f(X)，输入数据X是多少就可以投影得到唯一的一个Y，就是判决结果（算硬分类hard
assignment）。回到GMM，学习的过程就是训练出几个概率分布，所谓混合高斯模型就是指对样本的概率密度分布进行估计，而估计的模型是几个高斯模型加权之和（具体是几个要在模型训练前建立好）。每个高斯模型就代表了一个类（一个Cluster）。对样本中的数据分别在几个高斯模型上投影，就会分别得到在各个类上的概率。然后我们可以选取概率最大的类所为判决结果。

    得到概率有什么好处呢？我们知道人很聪明，就是在于我们会用各种不同的模型对观察到的事物和现象做判决和分析。当你在路上发现一条狗的时候，你可能光看外形好像邻居家的狗，又更像一点点女朋友家的狗，你很难判断，所以从外形上看，用软分类的方法，是女朋友家的狗概率51%，是邻居家的狗的概率是49%，属于一个易混淆的区域内，这时你可以再用其它办法进行区分到底是谁家的狗。而如果是硬分类的话，你所判断的就是女朋友家的狗，没有“多像”这个概念，所以不方便多模型的融合。

    从中心极限定理的角度上看，把混合模型假设为高斯的是比较合理的，当然也可以根据实际数据定义成任何分布的Mixture Model,不过定义为高斯的在计算上有一些方便之处，另外，理论上可以通过增加Model的个数，用GMM近似任何概率分布。

    混合高斯模型的定义为：

   

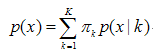
    其中K为模型的个数，πk为第k个高斯的权重，则为第k个高斯的概率密度函数，其均值为μk，方差为σk。我们对此概率密度的估计就是要求πk、μk和σk各个变量。当求出的表达式后，求和式的各项的结果就分别代表样本x属于各个类的概率。

    在做参数估计的时候，常采用的方法是最大似然。最大似然法就是使样本点在估计的概率密度函数上的概率值最大。由于概率值一般都很小，N很大的时候这个连乘的结果非常小，容易造成浮点数下溢。所以我们通常取log，将目标改写成：

  

    也就是最大化log-likelyhood function，完整形式则为：

    一般用来做参数估计的时候，我们都是通过对待求变量进行求导来求极值，在上式中，log函数中又有求和，你想用求导的方法算的话方程组将会非常复杂，所以我们不好考虑用该方法求解（没有闭合解）。可以采用的求解方法是EM算法——将求解分为两步：第一步是假设我们知道各个高斯模型的参数（可以初始化一个，或者基于上一步迭代结果），去估计每个高斯模型的权值；第二步是基于估计的权值，回过头再去确定高斯模型的参数。重复这两个步骤，直到波动很小，近似达到极值（注意这里是个极值不是最值，EM算法会陷入局部最优）。具体表达如下：

  

    1、对于第i个样本xi来说，它由第k个model生成的概率为：

   

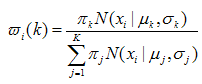
    在这一步，我们假设高斯模型的参数和是已知的（由上一步迭代而来或由初始值决定）。

   （E step）


   

    （M step）


    3、重复上述两步骤直到算法收敛（这个算法一定是收敛的，至于具体的证明请回溯到EM算法中去，而我也没有具体关注，以后补上）。


 

    最后总结一下，用GMM的优点是投影后样本点不是得到一个确定的分类标记，而是得到每个类的概率，这是一个重要信息。GMM每一步迭代的计算量比较大，大于k-means。GMM的求解办法基于EM算法，因此有可能陷入局部极值，这和初始值的选取十分相关了。GMM不仅可以用在聚类上，也可以用在概率密度估计上。

1）任意数据分布可用高斯混合模型（M个单高斯）表示（（1）式）

（1）

其中：

    （2）

   （3）   表示第j个高斯混合模型

2）N个样本集X的log似然函数如下：

     （4）

其中：

参数：，   （5）


下面具体讲讲基于EM迭代的混合高斯模型参数求解算法流程：

1）初始参数由k-means（其实也是一种特殊的高斯混合模型）决定：

[plain]
view plaincopy
  1. function [Priors, Mu, Sigma] = EM_init_kmeans(Data, nbStates)  
  2. % Inputs -----------------------------------------------------------------  
  3. %   o Data:     D x N array representing N datapoints of D dimensions.  
  4. %   o nbStates: Number K of GMM components.  
  5. % Outputs ----------------------------------------------------------------  
  6. %   o Priors:   1 x K array representing the prior probabilities of the  
  7. %               K GMM components.  
  8. %   o Mu:       D x K array representing the centers of the K GMM components.  
  9. %   o Sigma:    D x D x K array representing the covariance matrices of the   
  10. %               K GMM components.  
  11. % Comments ---------------------------------------------------------------  
  12. %   o This function uses the 'kmeans' function from the MATLAB Statistics   
  13. %     toolbox. If you are using a version of the 'netlab' toolbox that also  
  14. %     uses a function named 'kmeans', please rename the netlab function to  
  15. %     'kmeans_netlab.m' to avoid conflicts.   
  16.   
  17. [nbVar, nbData] = size(Data);  
  18.   
  19. %Use of the 'kmeans' function from the MATLAB Statistics toolbox  
  20. [Data_id, Centers] = kmeans(Data', nbStates);   
  21. Mu = Centers';  
  22. for i=1:nbStates  
  23.   idtmp = find(Data_id==i);  
  24.   Priors(i) = length(idtmp);  
  25.   Sigma(:,:,i) = cov([Data(:,idtmp) Data(:,idtmp)]');  
  26.   %Add a tiny variance to avoid numerical instability  
  27.   Sigma(:,:,i) = Sigma(:,:,i) + 1E-5.*diag(ones(nbVar,1));  
  28. end  
  29. Priors = Priors ./ sum(Priors);  

2）E步（求期望）

求取：

（7）

其实，这里最贴切的式子应该是log似然函数的期望表达式

事实上，3）中参数的求取也是用log似然函数的期望表达式求偏导等于0解得的简化后的式子，而这些式子至于（7）式有关，于是E步可以只求（7）式，以此简化计算，不需要每次都求偏导了。

[plain]
view plaincopy
  1. %% E-step %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%  
  2. for i=1:nbStates  
  3.   %Compute probability p(x|i)  
  4.   Pxi(:,i) = gaussPDF(Data, Mu(:,i), Sigma(:,:,i));  
  5. end  
  6. %Compute posterior probability p(i|x)  
  7. Pix_tmp = repmat(Priors,[nbData 1]).*Pxi;  
  8. Pix = Pix_tmp ./ repmat(sum(Pix_tmp,2),[1 nbStates]);  
  9. %Compute cumulated posterior probability  
  10. E = sum(Pix);  
[plain]
view plaincopy
  1. function prob = gaussPDF(Data, Mu, Sigma)  
  2. % Inputs -----------------------------------------------------------------  
  3. %   o Data:  D x N array representing N datapoints of D dimensions.  
  4. %   o Mu:    D x K array representing the centers of the K GMM components.  
  5. %   o Sigma: D x D x K array representing the covariance matrices of the   
  6. %            K GMM components.  
  7. % Outputs ----------------------------------------------------------------  
  8. %   o prob:  1 x N array representing the probabilities for the   
  9. %            N datapoints.       
  10.   
  11. [nbVar,nbData] = size(Data);  
  12.   
  13. Data = Data' - repmat(Mu',nbData,1);  
  14. prob = sum((Data*inv(Sigma)).*Data, 2);  
  15. prob = exp(-0.5*prob) / sqrt((2*pi)^nbVar * (abs(det(Sigma))+realmin));  

3）M步（最大化步骤）

更新权值：


更新均值：


更新方差矩阵：


[cpp]
view plaincopy
  1. %% M-step %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%  
  2.  for i=1:nbStates  
  3.    %Update the priors  
  4.    Priors(i) = E(i) / nbData;  
  5.    %Update the centers  
  6.    Mu(:,i) = Data*Pix(:,i) / E(i);  
  7.    %Update the covariance matrices  
  8.    Data_tmp1 = Data - repmat(Mu(:,i),1,nbData);  
  9.    Sigma(:,:,i) = (repmat(Pix(:,i)',nbVar, 1) .* Data_tmp1*Data_tmp1') / E(i);  
  10.    %% Add a tiny variance to avoid numerical instability  
  11.    Sigma(:,:,i) = Sigma(:,:,i) + 1E-5.*diag(ones(nbVar,1));  
  12.  end  

4）截止条件

不断迭代EM步骤，更新参数，直到似然函数前后差值小于一个阈值，或者参数前后之间的差（一般选择欧式距离）小于某个阈值，终止迭代，这里选择前者。附上结合EM步骤的代码：

[cpp]
view plaincopy
  1. while 1  
  2.   %% E-step %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%  
  3.   for i=1:nbStates  
  4.     %Compute probability p(x|i)  
  5.     Pxi(:,i) = gaussPDF(Data, Mu(:,i), Sigma(:,:,i));  
  6.   end  
  7.   %Compute posterior probability p(i|x)  
  8.   Pix_tmp = repmat(Priors,[nbData 1]).*Pxi;  
  9.   Pix = Pix_tmp ./ repmat(sum(Pix_tmp,2),[1 nbStates]);  
  10.   %Compute cumulated posterior probability  
  11.   E = sum(Pix);  
  12.   %% M-step %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%  
  13.   for i=1:nbStates  
  14.     %Update the priors  
  15.     Priors(i) = E(i) / nbData;  
  16.     %Update the centers  
  17.     Mu(:,i) = Data*Pix(:,i) / E(i);  
  18.     %Update the covariance matrices  
  19.     Data_tmp1 = Data - repmat(Mu(:,i),1,nbData);  
  20.     Sigma(:,:,i) = (repmat(Pix(:,i)',nbVar, 1) .* Data_tmp1*Data_tmp1') / E(i);  
  21.     %% Add a tiny variance to avoid numerical instability  
  22.     Sigma(:,:,i) = Sigma(:,:,i) + 1E-5.*diag(ones(nbVar,1));  
  23.   end  
  24.   %% Stopping criterion %%%%%%%%%%%%%%%%%%%%  
  25.   for i=1:nbStates  
  26.     %Compute the new probability p(x|i)  
  27.     Pxi(:,i) = gaussPDF(Data, Mu(:,i), Sigma(:,:,i));  
  28.   end  
  29.   %Compute the log likelihood  
  30.   F = Pxi*Priors';  
  31.   F(find(F<realmin)) = realmin;  
  32.   loglik = mean(log(F));  
  33.   %Stop the process depending on the increase of the log likelihood   
  34.   if abs((loglik/loglik_old)-1) < loglik_threshold  
  35.     break;  
  36.   end  
  37.   loglik_old = loglik;  
  38.   nbStep = nbStep+1;  
  39. end  

结果测试（第一幅为样本点集，第二幅表示求取的高斯混合模型，第三幅为回归模型）：



忘了说了，传统的GMM和k-means一样，需要给定K值（即:要有几个高斯函数）。

返回
【上篇】
【下篇】

作者:

抱歉!评论已关闭.

返回首页

Copyright © 2013-2018 学步园  保留所有权利.
软文销售 QQ客服：2265327166 点击这里给我发消息（其他合作也可洽谈）
必威体育
必威电竞