1) 多邊形面积
http://zh.wikipedia.org/zh-tw/%E5%A4%9A%E8%BE%B9%E5%BD%A2#.E9.9D.A2.E7.A7.AF
面積
對用 (按逆時針排列)描述的多邊形,其面積為:
(按逆時針排列)描述的多邊形,其面積為:
若按順時針排列,取負數即可。
對用邊長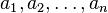 和外角
和外角 描述的多邊形,其面積為:
描述的多邊形,其面積為:
用邊長和內角描述如下 N邊形S=∑[(-1)^k*mnsinθ]/2這個代表N邊形已知(N-1)個邊的長度,而且知道其中任意兩邊的夾角,對於這兩邊 (-1)^k*mnsinθ求和後的一半便是面積 註明:K=0或1,目的是為了表明每個因式mnsinθ的正負號與M,N的交點位置有關
2) 判斷一個點是否在凸多邊形內部 射線演算法
多边形填充Polygon Filling ,flood fill算法,裝填凸多邊形( Scanline Fill Algorithm ),裝填簡單多邊形參考: http://alienryderflex.com/polygon_fill/ 。原理與 Point in Polygon 的演算法是一樣的,另一種很常用的方式,是將簡單多邊形進行三角化,每個三角形各自裝填。,延伸閱讀: Pick's Theorem
http://www.csie.ntnu.edu.tw/~u91029/Polygon.html
3) 判断多边形的方向是顺时针还是逆时针
http://hi.baidu.com/cityhacker/blog/item/ad9e1b82aba5cea50cf4d2a7.html
4) Flood-Fill 种子填充
http://hi.baidu.com/richardma_/blog/item/d688828b9e29c9be0f2444a9.html
问题描述
给出一个点,一张图,算法目的是将该点及其周围同颜色点的颜色替换为某种颜色
算法描述
Flood-fill(点坐标,目标颜色,替换颜色)
1. 如果坐标上的颜色不是目标颜色,则退出
2. 将坐标点设置为替换颜色
3. 递归调用Flood-fill,填充左侧坐标
递归调用Flood-fill,填充右侧坐标
递归调用Flood-fill,填充上方坐标
递归调用Flood-fill,填充下方坐标
4. 返回
5) Floyd-Warshall算法(Floyd-Warshall algorithm)是解決任意兩點間的最短路徑的一種算法,可以正確處理有向圖或負權的最短路徑問題。
http://zh.wikipedia.org/zh-hk/%E5%BC%97%E6%B4%9B%E4%BC%8A%E5%BE%B7%E7%AE%97%E6%B3%95
Floyd-Warshall算法的原理是動態規劃。
設Di,j,k為從i到j的只以(1..k)集合中的節點為中間節點的最短路徑的長度。
- 若最短路徑經過點k,則Di,j,k = Di,k,k − 1 + Dk,j,k − 1;
- 若最短路徑不經過點k,則Di,j,k = Di,j,k − 1。
因此,Di,j,k = min(Di,k,k − 1 + Dk,j,k − 1,Di,j,k − 1)。
在實際算法中,為了節約空間,可以直接在原來空間上進行迭代,這樣空間可降至二維。(見下面的算法描述)
[編輯] 算法描述
Floyd-Warshall算法的描述如下:
for k ← 1 to n do
for i ← 1 to n do
for j ← 1 to n do
if (Di,k + Dk,j < Di,j) then
Di,j← Di,k + Dk,j;
其中Di,j表示由點i到點j的代價,當Di,j為 ∞ 表示兩點之間沒有任何連接。
6) Dijkstra算法
7) 最短路問題
http://zh.wikipedia.org/zh-hk/%E5%9B%BE%E8%AE%BA%E6%9C%80%E7%9F%AD%E8%B7%AF
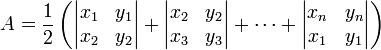
![\begin{align}A = \frac12 ( a_1[a_2 \sin(\theta_1) + a_3 \sin(\theta_1 + \theta_2) + \cdots + a_{n-1} \sin(\theta_1 + \theta_2 + \cdots + \theta_{n-2})] \\ {} + a_2[a_3 \sin(\theta_2) + a_4 \sin(\theta_2 + \theta_3) + \cdots + a_{n-1} \sin(\theta_2 + \cdots + \theta_{n-2})] \\ {} + \cdots + a_{n-2}[a_{n-1} \sin(\theta_{n-2})] ) \end{align}](http://upload.wikimedia.org/math/b/1/c/b1c72b33d267eb9f1caece94e029b84e.png)