第十五章 三角Bézier曲面
在第十章、第十一章和第十二章,我们介绍了双三次Hermite曲面、Bézier曲面和B样条曲面等。无论其构成方式如何,都是定义在矩形参数域上,并且给定的数据信息具有矩形拓扑结构,曲面片具有四条边界。然而,在实际工程应用中,并不是所有给定的数据信息都具备矩形拓扑结构,或者说,并非所有的形体表面都仅能通过使用四边曲面片来表示。那么就需要引入三角曲面片。三角曲面片和四边曲面片除了拓扑结构不同外,并没有其他本质上的区别。在四边曲面中,参数 和参数域由矩形区域
和参数域由矩形区域 定义,在三角曲面中,其参数则由重心坐标给出。
定义,在三角曲面中,其参数则由重心坐标给出。
三角域上的多项式曲面首先由de Casteljau于1959年引入。以另外的形式,比方Lagrange形式广泛用于有限元分析之中。其最常用的方法是Clough-Tocher方法和五次二十一参数插值方法。二十世纪七十年代,出现了许多三角曲面插值方法,如BBG插值方法、三角Bézier曲面片、多元B样条、Box样条等。三角曲面片技术主要用于非规则形体的建模和散乱数据的数值处理,象实验数据处理、地形图生成当中的无噪声插值、有噪声拟合等等。在三角曲面技术中,应用组为广泛的是三角Bézier曲面片,它是按照定义在规则三角剖分上的二元Bernstein基函数来构造曲面的。本章将主要就这种三角曲面片及其相关技术予以介绍和讨论。
14.1 重心坐标
在平面上可以建立各种坐标系,使其几何点与代数有序数组一一对应。当选用笛卡尔坐标系时,便得到了常用的直角坐标。如果选择仿射坐标系,则引入点的重心坐标。

给定平面上不共线的三个点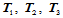 ,那么可构成一三角形
,那么可构成一三角形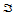 ,从而平面上任一点
,从而平面上任一点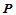 可表示为:
可表示为:
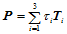
(14.1.1)
三元组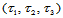 称为点
称为点 相应于三角形
相应于三角形 的重心坐标,满足条件:
的重心坐标,满足条件:
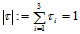
(14.1.2)
重心坐标的物理意义是质心,它与直角坐标的关系是:

可通过三角形的有向面积计算如下:
 (14.1.3)
(14.1.3)
其中:
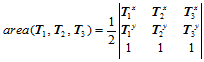
按其字母顺序,顺时针旋转为正,逆时针旋转为负。
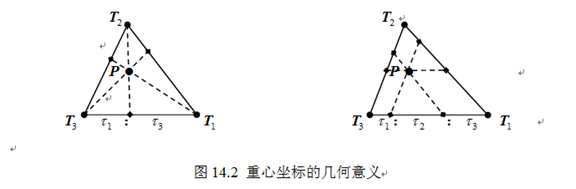
重心坐标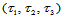 的几何意义除了是有向面积比之外,还描述了过点
的几何意义除了是有向面积比之外,还描述了过点
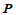 的直线所产生的一些比例关系,如图14.2所示。
的直线所产生的一些比例关系,如图14.2所示。
此外,按照重心坐标 中分量的符号将平面分成七个区域(图14.3)。特别,三角形
中分量的符号将平面分成七个区域(图14.3)。特别,三角形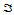 三个顶点
三个顶点 的重心坐标分别是:
的重心坐标分别是: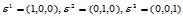 。
。
重心坐标最为重要的性质之一是仿射不变性:如果三角形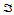 和点
和点 经过仿射变换变成另一个三角形
经过仿射变换变成另一个三角形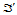 和点
和点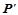 ,那么点
,那么点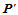 相对于
相对于 的重心坐标等于点
的重心坐标等于点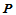 相应于三角形
相应于三角形 的重心坐标。
的重心坐标。

证明 设 是一仿射变换,则
是一仿射变换,则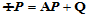 ,其中
,其中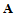 是三阶方阵,
是三阶方阵,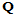 是列向量。则:
是列向量。则:

这有两层含义,其一是在同一平面进行仿射变换,将三角形 变换成
变换成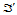 ;其二是在两张平面间进行仿射变换,将三角形
;其二是在两张平面间进行仿射变换,将三角形 变换成另一张平面内的三角形
变换成另一张平面内的三角形 。
。
如果我们考虑定义在三角形上的一个二元函数 ,那么我们面临的问题便是:怎样进行微分运算。此时,
,那么我们面临的问题便是:怎样进行微分运算。此时, 并没有几何解释。因此,这里引入方向导数。设
并没有几何解释。因此,这里引入方向导数。设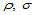 是平面内任意两点,那么
是平面内任意两点,那么 便定义了平面内一方向
便定义了平面内一方向 。方向
。方向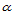 的重心坐标
的重心坐标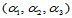 满足条件:
满足条件:

(14.1.4)
为了区别于点的重心坐标,方向的重心坐标称为零心坐标。函数 关于方向
关于方向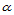 的方向导数则为:
的方向导数则为:
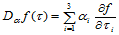
(14.1.5)
因此,今后凡处理用重心坐标表示的函数时,我们用方向导数代替偏导数。当然,方向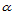 不必是单位长度。
不必是单位长度。
14.2 Lagrange插值
我们知道,一元多项式的最重要的应用之一就是插值。那么,在一三角形上怎样进行多项式插值呢?为此,就需要将一元情形下的节点序列推广到二元情形。
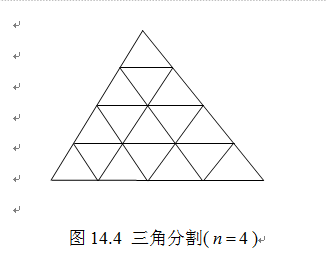
令 ,那么点
,那么点 便构成三角形
便构成三角形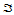 的一个分割,
的一个分割,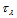 称为节点(图14.4)。在节点
称为节点(图14.4)。在节点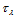 处给定数据
处给定数据 ,我们的目的是构造一
,我们的目的是构造一 次二元多项式
次二元多项式 ,使其满足条件:
,使其满足条件:
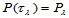
这里,由于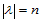 ,所以给定的数据
,所以给定的数据 共有
共有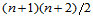 ─称之为三角数。
─称之为三角数。
要求的二元多项式表示如下:
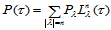
(14.2.1)
其中
 (14.2.2)
(14.2.2)
为了证明其正确性,只需验证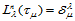 即可。由此二元多项式
即可。由此二元多项式 构成了三角形
构成了三角形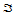 上
上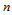 次二元多项式空间的基底,称为二元Lagrange基函数。
次二元多项式空间的基底,称为二元Lagrange基函数。
插值多项式 的计算可采用以下的递推公式:
的计算可采用以下的递推公式:
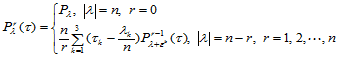 (14.2.3)
(14.2.3)
那么, 。
。
沿着 的边界,插值公式(14.2.1)便退化为一元Lagrange插值公式。当
的边界,插值公式(14.2.1)便退化为一元Lagrange插值公式。当 时,便得到线性插值。
时,便得到线性插值。
14.3 三角Bézier曲面的定义及性质
14.3.1 二元Bernstein多项式
三角域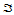 上的
上的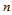 次Bernstein多项式定义如下:
次Bernstein多项式定义如下:
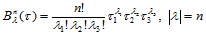 (14.3.1)
(14.3.1)
我们约定,当 时,
时,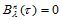 。
。
由于二元Bernstein多项式是三项式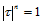 展开式中的各项,因此具有归一性:
展开式中的各项,因此具有归一性:
 (14.3.2)
(14.3.2)
当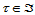 时,
时, 。当
。当 时,
时, 取得最大值。
取得最大值。
14.3.2 三角Bézier曲面的定义与性质
给定三角域 上的分割
上的分割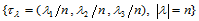 ,及节点
,及节点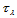 处的数值
处的数值 ,二元函数:
,二元函数:
 (14.3.3)
(14.3.3)
称为定义在三角形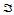 上的
上的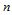 次三角Bézier曲面,其中
次三角Bézier曲面,其中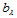 称为曲面
称为曲面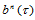 的Bézier纵标,有空间点
的Bézier纵标,有空间点 构成的分片线性曲面BL叫做
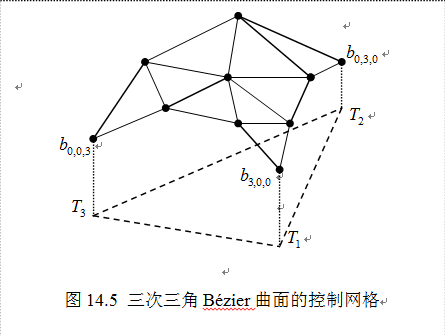
构成的分片线性曲面BL叫做 的控制网格或Bézier网。例如,三次三角Bézier曲面的Bézier网如图14.4所示。
的控制网格或Bézier网。例如,三次三角Bézier曲面的Bézier网如图14.4所示。
三角Bézier曲面具有以下重要性质:
1. 凸包性。 位于定义它的Bézier网的凸包之中,即:
位于定义它的Bézier网的凸包之中,即:

2. 角点性质。曲面通过Bézier网的三个角点,即:
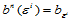
 在
在 处的切平面为点
处的切平面为点 确定的平面,在
确定的平面,在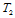 处的切平面由点
处的切平面由点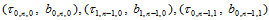 所确定,在
所确定,在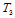 处的切平面则由点
处的切平面则由点
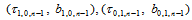 确定。
确定。
3. 边界性质。若记 ,则:
,则: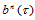 在边界
在边界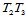 上是一
上是一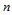 次Bézier曲线,即:
次Bézier曲线,即:
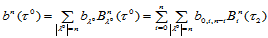
对于边界 、
、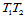 也有类似的结果。
也有类似的结果。
14.4 三角Bézier曲面的升阶
同张量积Bézier曲面一样,三角Bézier曲面也具有相应的升阶性质。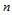 次三角Bézier曲面
次三角Bézier曲面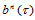 形式上可表示为
形式上可表示为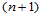 次三角Bézier曲面。
次三角Bézier曲面。
定理14.1
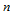 次三角Bézier曲面
次三角Bézier曲面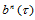 形式上可表示为
形式上可表示为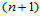 次三角Bézier曲面:
次三角Bézier曲面:
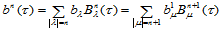 (14.4.1)
(14.4.1)
其中:
 (14.4.2)
(14.4.2)
证明 由于
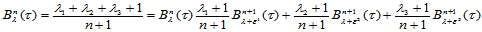
将其代入 的表达式中,整理即得。
的表达式中,整理即得。
式(14.4.2)的几何解释是:Bézier纵标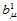 是Bézier网BL在点
是Bézier网BL在点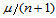 处的值,即:
处的值,即:

如果我们反复进行升阶,会产生怎样的结果呢?令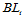 为第
为第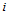 次升阶后的Bézier网,由于每一个
次升阶后的Bézier网,由于每一个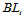 都是定义在同一三角域
都是定义在同一三角域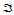 上的分片线性函数,且定义了相同的三角Bézier曲面
上的分片线性函数,且定义了相同的三角Bézier曲面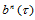 。
。 的顶点由下式确定:
的顶点由下式确定:
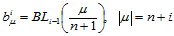 (14.4.3)
(14.4.3)
定理14.2
经过第 次升阶后,
次升阶后,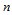 次三角Bézier曲面
次三角Bézier曲面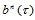 形式上可表示为
形式上可表示为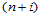 次的三角Bézier曲面:
次的三角Bézier曲面:
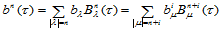 (14.4.4)
(14.4.4)
其中:
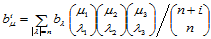 (14.4.5)
(14.4.5)
这里约定当 时,组合系数
时,组合系数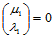 。
。
证明
 时,
时,
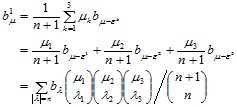
结论成立。
假设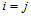 时结论成立,则当
时结论成立,则当 时,由升阶公式可知:
时,由升阶公式可知:
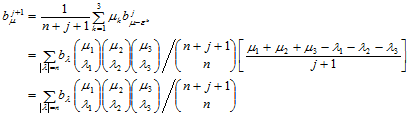
根据归纳法,结论成立。
当然,也可通过在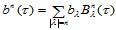 两边乘以
两边乘以 ,然后重新排列来证明该定理。
,然后重新排列来证明该定理。
如果升阶过程无限进行下去,那么Bézier网 将收敛到三角Bézier曲面片
将收敛到三角Bézier曲面片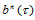 ,即有下面的定理。
,即有下面的定理。
定理14.3
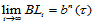
为了证明这一结论,我们引入引理。
引理14.1
若存在序列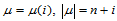 ,满足条件:
,满足条件:
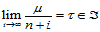
则: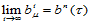 。
。
证明 由式(14.4.5)可知:

另一方面,
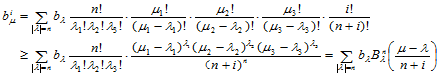
即:
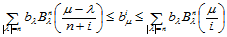
由于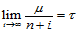 ,故
,故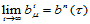 。
。
现在,我们证明定理14.3。
由于点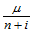 在三角形
在三角形 中是稠密的,那么对
中是稠密的,那么对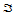 中任意一点
中任意一点 都存在序列
都存在序列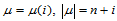 ,使得:
,使得:
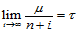
由引理14.1,对应的Bézier纵标序列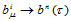 ,即:
,即:
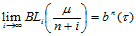
14.5 三角Bézier曲面的de Casteljau算法
类似于张量积Bézier曲面上点的计算,三角Bézier曲面上的点的计算亦可由一系列线性插值来完成,对应的算法称之为de Casteljau算法。
引理14.2 二元Bernstein基函数满足以下递推公式:
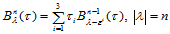 (14.5.1)
(14.5.1)
定理14.4
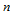 次三角Bézier曲面
次三角Bézier曲面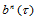 可形式上表示为:
可形式上表示为:
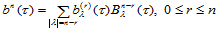 (14.5.2)
(14.5.2)
其中:
 (14.5.3)
(14.5.3)
当 时,有
时,有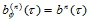 。这便是计算三角Bézier曲面上一点值的de Casteljau算法。
。这便是计算三角Bézier曲面上一点值的de Casteljau算法。
证明
 时,结论显然成立。
时,结论显然成立。
 时,由基函数的递推公式,可知:
时,由基函数的递推公式,可知:
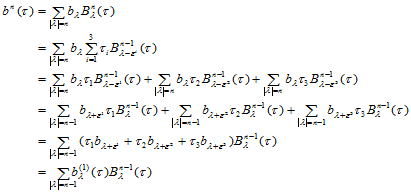
假设 时结论成立,即:
时结论成立,即:
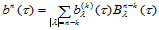
那么,当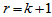 时
时
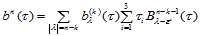
由归纳法假设,有:
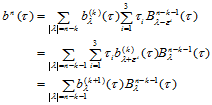
故结论成立。
递推公式(14.5.3)的几何解释是:点 是将域三角形
是将域三角形 仿射变换为三角曲面
仿射变换为三角曲面 的Bézier网上的三角形时,点
的Bézier网上的三角形时,点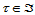 的仿射像。因此,Bézier曲面片在仿射下不变。这表明,如果用de Casteljau算法计算
的仿射像。因此,Bézier曲面片在仿射下不变。这表明,如果用de Casteljau算法计算 ,然后将其进行仿射变换,与先对
,然后将其进行仿射变换,与先对 的Bézier网进行仿射变换,再在新的Bézier网中用de Casteljau算法计算,其结果一致。特别,若令
的Bézier网进行仿射变换,再在新的Bézier网中用de Casteljau算法计算,其结果一致。特别,若令 ,则有:
,则有:

式(14.5.3)中的中间点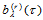 具有下面的显式表示:
具有下面的显式表示:

(14.5.4)
证明
 时,有:
时,有:

假设 时结论成立,即:
时结论成立,即:

则当 时,有
时,有

故结论成立。
14.6 三角Bézier曲面的方向导数
给定一方向 ,记二元函数
,记二元函数 的偏导数的重心坐标表示为
的偏导数的重心坐标表示为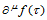 ,即:
,即:

那么,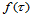 关于
关于 的
的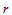 阶方向导数是:
阶方向导数是:
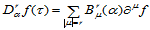
(14.6.1)
证明
 时,根据方向导数的定义,有:
时,根据方向导数的定义,有:
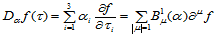
假设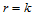 时结论成立,则当
时结论成立,则当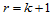 时,有:
时,有:
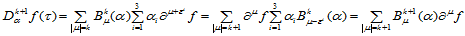
证毕。
值得注意的是,尽管 ,但
,但 有意义,即:
有意义,即:
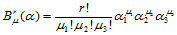
这是一形式表示。
特别,若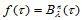 ,那么
,那么

由此可得三角Bézier曲面方向导数的计算公式。
定理14.5 二元Bernstein基函数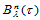 关于方向
关于方向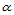 的
的 阶方向导数是:
阶方向导数是:
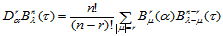
(14.6.2)
定理14.6 三角Bézier曲面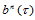 关于方向
关于方向 的
的 阶方向导数是:
阶方向导数是:

(14.6.3)
证明 由定理14.5,可知:
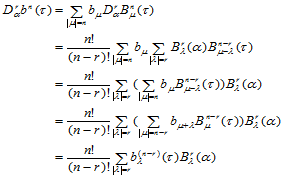
式(14.6.3)的几何解释是:当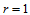 时,三点
时,三点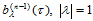 ,确定了三角Bézier曲面
,确定了三角Bézier曲面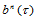 在
在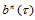 处的切平面。
处的切平面。
推论14.1
 (14.6.4)
(14.6.4)
证明
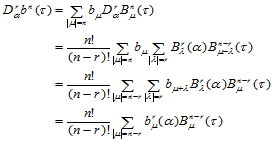
式(14.6.4)的一个简单几何解释是:当 时,
时,
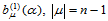 ,表示由三点
,表示由三点 所确定在方向
所确定在方向 上的斜率。
上的斜率。
式(14.6.3)和(14.6.4)可解释如下:如果按照(14.6.3)计算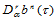 ,则首先对参数
,则首先对参数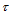 做
做 级de Casteljau递归,求得
级de Casteljau递归,求得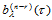 ,然后对
,然后对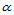 做
做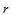 级de Casteljau递归即可。用(14.6.4)计算
级de Casteljau递归即可。用(14.6.4)计算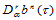 ,则恰好倒过来,先对
,则恰好倒过来,先对 做
做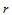 级de Casteljau递归求得
级de Casteljau递归求得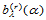 ,再对
,再对 做
做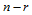 级de Casteljau递归。也就是说,求值的递归与求导数的递归可交换,只要分别对
级de Casteljau递归。也就是说,求值的递归与求导数的递归可交换,只要分别对 和
和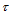 做
做 级与
级与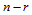 级de Casteljau递归,不管以什么样的次序进行。
级de Casteljau递归,不管以什么样的次序进行。
对于域三角形 的一条边界,比如
的一条边界,比如 和一与其不平行的方向
和一与其不平行的方向 ,其相应的
,其相应的 阶方向导数为:
阶方向导数为:
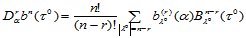
(14.6.5)
它仅依赖于与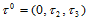 平行的邻近
平行的邻近 排Bézier纵标。
排Bézier纵标。
将式(14.6.3)和(14.6.4)推广,便可得到混合方向导数的计算公式。令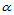 和
和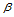 是两个互不平行的方向,则:
是两个互不平行的方向,则:
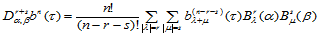
(14.6.6)

(14.6.7)
这里,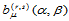 表示对
表示对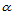 做
做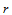 级de Casteljau递归,然后对
级de Casteljau递归,然后对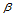 做
做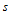 级de Casteljau递归,即:
级de Casteljau递归,即:

在域三角形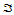 的顶点处,混合方向导数仅与顶点处的
的顶点处,混合方向导数仅与顶点处的 阶子网相关。
阶子网相关。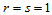 时,相应的混合方向导数称做"扭矢"。此时,若
时,相应的混合方向导数称做"扭矢"。此时,若 、
、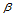 与域三角形的边平行,则称之为边扭矢。例如,
与域三角形的边平行,则称之为边扭矢。例如, 时,则有:
时,则有:

(14.6.8)
其中,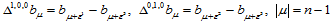 。
。
式(14.6.8)的几何意义如下:
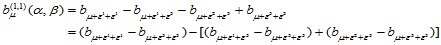
根据以上的讨论,可得到三角域上Bézier曲面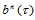 关于三个变元的偏导数计算公式。
关于三个变元的偏导数计算公式。
定理14.7 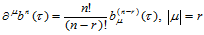
(14.6.9)
证明

特别,当 时,则有:
时,则有: