学步园

§7 两矢量的数性积

 

定义1 对于两个矢量a和b,把它们的模|a|,|b|及它们的夹角q 的余弦的乘积称为矢量和的数量积,记作ab,即

ab=|a||b|cosq .

由此定义和投影的关系可得

ab=|b|Prj_b
a=|a|Prj_ab.

数量积的性质:

(1) a·a=|a| ²,记a·a=a ²，则a²=|a| ².

(2) 对于两个非零矢量 a、b,如果 a·b=0,则 a^b

反之,如果a^b,则a·b=0.

如果认为零矢量与任何矢量都垂直,则a^bÛa·b=0.

定理1 数量积满足下面运算律：

(1)交换律: a·b=
b·a

(2)分配律:(a+b)×c=a×c+b×c
.

(3)(la)·b=
a·(lb)=
l(a·b),

(la)·(mb)=
lm(a·b),l、m为数.

证 （1）由定义知显然.

(2)的证明:

因为当c=0时, 上式显然成立;

当c¹0时, 有

(a+b)×c=|c|Prj_c(a+b)

=|c|(Prj_ca+Prj_cb)

=|c|Prj_ca+|c|Prj_cb

=a×c+b×c
.

（3）可类似地证明.

例1 试用矢量证明三角形的余弦定理.

证 设在ΔABC中,∠BCA=,||=a, ||=b, ||=c, 要证

c ²=a ²+b ²-2 a
b cos .

记=a,=b,=c,则有 c=a-b, 从而

|c|²=c
×
c=(a-b)(a-b)=a²-2×ab+b²=|a|²+|b|²-2|a||b|cos(a,^b),

即 c ²=a ²+b ²-2 a
b cos .



数量积的坐标表示:

定理2 设a={a_x,
a_y,
a_z },b={b_x,
b_y,
b_z }, 则

a·b=a_xb_x+a_yb_y+a_zb_z .

证 a·b=( a_x i+
a_y j +
a_z k)·(b_x i +
b_y j +
b_z k)

=a_x
b_x i·i +
a_x b_y i·j +
a_x b_z i·k

+a_y
b_x j ·i +
a_y b_y j ·j +
a_y b_z j·k

+a_z
b_x k·i +
a_z b_y k·j +
a_z b_z k·k

= a_x
b_x
+ a_y b_y
+ a_z b_z .

定理3 设a={},则矢量a的模

|a|=.

证 由定理1.7.2知

|a|²=a²=，

所以 |a|=.

两矢量夹角的余弦的坐标表示:

定理4

设q=(a, ^ b), 则当a¹0、b¹0时,有

.

证 因为 a·b=|a||b|cosq
，所以

.

 

例2 已知三点M (1,1,1)、A (2,2,1)和B (2,1,2),求ÐAMB
.

解 从M到A的向量记为a, 从M到B的向量记为b, 则ÐAMB 就是向量a与b的夹角.

a={1,1,0},b={1,0,1}.

因为

a×b=1´1+1´0+0´1=1,

,

.

所以 .

从而 .

矢量的方向角和方向余弦：矢量与坐标轴所成的角叫做矢量的方向角，方向角的余弦叫矢量的方向余弦.

定理5 设a={}，则a的方向余弦为

cos=,

cos,

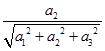cos；

且 ，

其中分别是矢量a与x轴，y轴,z轴的夹角.

证 因为 ai=|a|cos且ai=，

所以 |a|cos=，

从而 cos=.

同理可证 cos

 

cos

且显然