注:博客中图表的大小难以调整,导致阅读不便,这里有其pdf版本:高斯模糊实现小结.pdf
高斯模糊是一种图像滤波器,它使用正态分布(高斯函数)计算模糊模板,并使用该模板与原图像做卷积运算,达到模糊图像的目的。
N维空间正态分布方程为:

其中,σ是正态分布的标准差,σ值越大,图像越模糊(平滑)。r为模糊半径,模糊半径是指模板元素到模板中心的距离。如二维模板大小为m*n,则模板上的元素(x,y)对应的高斯计算公式为:

在二维空间中,这个公式生成的曲面的等高线是从中心开始呈正态分布的同心圆。分布不为零的像素组成的卷积矩阵与原始图像做变换。每个像素的值都是周围相邻像素值的加权平均。原始像素的值有最大的高斯分布值,所以有最大的权重,相邻像素随着距离原始像素越来越远,其权重也越来越小。这样进行模糊处理比其它的均衡模糊滤波器更高地保留了边缘效果。
理论上来讲,图像中每点的分布都不为零,这也就是说每个像素的计算都需要包含整幅图像。在实际应用中,在计算高斯函数的离散近似时,在大概3σ距离之外的像素都可以看作不起作用,这些像素的计算也就可以忽略。通常,图像处理程序只需要计算(6σ+1)*(6σ+1)的矩阵就可以保证相关像素影响。
1、使用给定高斯模板平滑图像函数
σ=0.84089642的7行7列高斯模糊矩阵为:
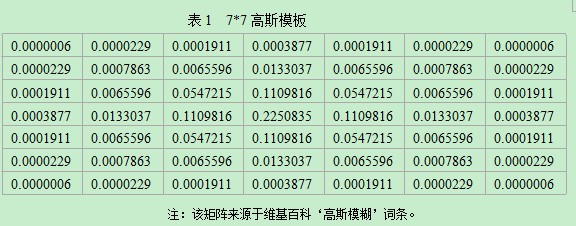
现使用该模板对源图像做模糊处理,其函数如下:
//高斯平滑
//未使用sigma,边缘无处理
void GaussianTemplateSmooth(const Mat &src, Mat &dst, double sigma)
{
//高斯模板(7*7),sigma = 0.84089642,归一化后得到
static const double gaussianTemplate[7][7] =
{
{0.00000067, 0.00002292, 0.00019117, 0.00038771, 0.00019117, 0.00002292, 0.00000067},
{0.00002292, 0.00078633, 0.00655965, 0.01330373, 0.00655965, 0.00078633, 0.00002292},
{0.00019117, 0.00655965, 0.05472157, 0.11098164, 0.05472157, 0.00655965, 0.00019117},
{0.00038771, 0.01330373, 0.11098164, 0.22508352, 0.11098164, 0.01330373, 0.00038771},
{0.00019117, 0.00655965, 0.05472157, 0.11098164, 0.05472157, 0.00655965, 0.00019117},
{0.00002292, 0.00078633, 0.00655965, 0.01330373, 0.00655965, 0.00078633, 0.00002292},
{0.00000067, 0.00002292, 0.00019117, 0.00038771, 0.00019117, 0.00002292, 0.00000067}
};
dst.create(src.size(), src.type());
uchar* srcData = src.data;
uchar* dstData = dst.data;
for(int j = 0; j < src.cols-7; j++)
{
for(int i = 0; i < src.rows-7; i++)
{
double acc = 0;
double accb = 0, accg = 0, accr = 0;
for(int m = 0; m < 7; m++)
{
for(int n = 0; n < 7; n++)
{
if(src.channels() == 1)
acc += *(srcData + src.step * (i+n) + src.channels() * (j+m)) * gaussianTemplate[m][n];
else
{
accb += *(srcData + src.step * (i+n) + src.channels() * (j+m) + 0) * gaussianTemplate[m][n];
accg += *(srcData + src.step * (i+n) + src.channels() * (j+m) + 1) * gaussianTemplate[m][n];
accr += *(srcData + src.step * (i+n) + src.channels() * (j+m) + 2) * gaussianTemplate[m][n];
}
}
}
if(src.channels() == 1)
*(dstData + dst.step * (i+3) + dst.channels() * (j+3))=(int)acc;
else
{
*(dstData + dst.step * (i+3) + dst.channels() * (j+3) + 0)=(int)accb;
*(dstData + dst.step * (i+3) + dst.channels() * (j+3) + 1)=(int)accg;
*(dstData + dst.step * (i+3) + dst.channels() * (j+3) + 2)=(int)accr;
}
}
}
}
其效果如图1所示,7*7的高斯模板与源图像做卷积运算时,会产生半径为3的边缘,在不精确的图像处理中,可用源图像像素填充,或者去掉边缘。

2、二维高斯模糊函数
上述的例子中,如何求得高斯模糊矩阵是高斯模糊的关键。根据高斯函数的性质,图像处理程序只需要计算(6σ+1)*(6σ+1)的矩阵就可以保证相关像素影响。因此,可根据σ的值确定高斯模糊矩阵的大小。高斯矩阵可利用公式(1-2)计算,并归一化得到。归一化是保证高斯矩阵的值在[0,1]之间,
其处理函数如下:
void GaussianSmooth2D(const Mat &src, Mat &dst, double sigma)
{
if(src.channels() != 1)
return;
//确保sigma为正数
sigma = sigma > 0 ? sigma : 0;
//高斯核矩阵的大小为(6*sigma+1)*(6*sigma+1)
//ksize为奇数
int ksize = cvRound(sigma * 3) * 2 + 1;
// dst.create(src.size(), src.type());
if(ksize == 1)
{
src.copyTo(dst);
return;
}
dst.create(src.size(), src.type());
//计算高斯核矩阵
double *kernel = new double[ksize*ksize];
double scale = -0.5/(sigma*sigma);
const double PI = 3.141592653;
double cons = -scale/PI;
double sum = 0;
for(int i = 0; i < ksize; i++)
{
for(int j = 0; j < ksize; j++)
{
int x = i-(ksize-1)/2;
int y = j-(ksize-1)/2;
kernel[i*ksize + j] = cons * exp(scale * (x*x + y*y));
sum += kernel[i*ksize+j];
// cout << " " << kernel[i*ksize + j];
}
// cout <<endl;
}
//归一化
for(int i = ksize*ksize-1; i >=0; i--)
{
*(kernel+i) /= sum;
}
//图像卷积运算,无边缘处理
for(int j = 0; j < src.cols-ksize; j++)
{
for(int i = 0; i < src.rows-ksize; i++)
{
double acc = 0;
for(int m = 0; m < ksize; m++)
{
for(int n = 0; n < ksize; n++)
{
acc += *(srcData + src.step * (i+n) + src.channels() * (j+m)) * kernel[m*ksize+n];
}
}
*(dstData + dst.step * (i + (ksize - 1)/2) + (j + (ksize -1)/2)) = (int)acc;
}
}
delete []kernel;
}
利用该函数,取σ=0.84089642即可得到上例中7*7的模板,该模板数据存在kernel中。利用该函数计算的归一化后的3*3,5*5阶高斯模板如表2,3所示:
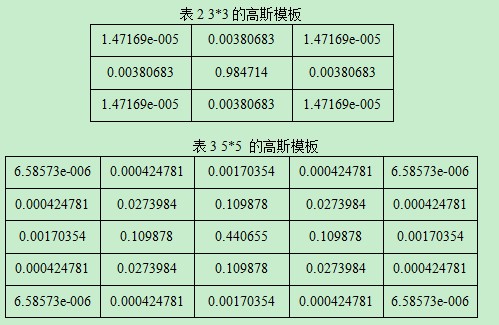
由上表可以看出,高斯模板是中心对称的。
模糊效果如图2所示。

对图2中边缘的处理:
...
int center = (ksize-1) /2;
//图像卷积运算,处理边缘
for(int j = 0; j < src.cols; j++)
{
for(int i = 0; i < src.rows; i++)
{
double acc = 0;
for(int m = -center, c = 0; m <= center; m++, c++)
{
for(int n = -center, r = 0; n <= center; n++, r++)
{
if((i+n) >=0 && (i+n) < src.rows && (j+m) >=0 && (j+m) < src.cols)
{
acc += *(srcData + src.step * (i+n) + src.channels() * (j+m)) * kernel[r*ksize+c];
}
}
}
*(dstData + dst.step * (i) + (j)) = (int)acc;
}
}
...
结果图为:

如上图所示,边缘明显变窄,但是存在黑边。
3、改进的高斯模糊函数
上述的二维高斯模糊函数GaussianSmooth2D达到了高斯模糊图像的目的,但是如图2所示,会因模板的关系而造成边缘图像缺失,σ越大,缺失像素越多,额外的边缘处理会增加计算量。并且当σ变大时,高斯模板(高斯核)和卷积运算量将大幅度提高。根据高斯函数的可分离性,可对二维高斯模糊函数进行改进。
高斯函数的可分离性是指使用二维矩阵变换得到的效果也可以通过在水平方向进行一维高斯矩阵变换加上竖直方向的一维高斯矩阵变换得到。从计算的角度来看,这是一项有用的特性,因为这样只需要O(n*M*n)+O(m*M*N)次计算,而二维不可分的矩阵则需要O(m*n*M*n)次计算,其中,m,n为高斯矩阵的维数,M,N为二维图像的维数。
另外,两次一维的高斯卷积将消除二维高斯矩阵所产生的边缘。
改进的高斯模糊函数如下:
void GaussianSmooth(const Mat &src, Mat &dst, double sigma)
{
if(src.channels() != 1 && src.channels() != 3)
return;
//
sigma = sigma > 0 ? sigma : -sigma;
//高斯核矩阵的大小为(6*sigma+1)*(6*sigma+1)
//ksize为奇数
int ksize = ceil(sigma * 3) * 2 + 1;
//cout << "ksize=" <<ksize<<endl;
// dst.create(src.size(), src.type());
if(ksize == 1)
{
src.copyTo(dst);
return;
}
//计算一维高斯核
double *kernel = new double[ksize];
double scale = -0.5/(sigma*sigma);
const double PI = 3.141592653;
double cons = 1/sqrt(-scale / PI);
double sum = 0;
int kcenter = ksize/2;
int i = 0, j = 0;
for(i = 0; i < ksize; i++)
{
int x = i - kcenter;
*(kernel+i) = cons * exp(x * x * scale);//一维高斯函数
sum += *(kernel+i);
// cout << " " << *(kernel+i);
}
// cout << endl;
//归一化,确保高斯权值在[0,1]之间
for(i = 0; i < ksize; i++)
{
*(kernel+i) /= sum;
// cout << " " << *(kernel+i);
}
// cout << endl;
dst.create(src.size(), src.type());
Mat temp;
temp.create(src.size(), src.type());
uchar* srcData = src.data;
uchar* dstData = dst.data;
uchar* tempData = temp.data;
//x方向一维高斯模糊
for(int y = 0; y < src.rows; y++)
{
for(int x = 0; x < src.cols; x++)
{
double mul = 0;
sum = 0;
double bmul = 0, gmul = 0, rmul = 0;
for(i = -kcenter; i <= kcenter; i++)
{
if((x+i) >= 0 && (x+i) < src.cols)
{
if(src.channels() == 1)
{
mul += *(srcData+y*src.step+(x+i))*(*(kernel+kcenter+i));
}
else
{
bmul += *(srcData+y*src.step+(x+i)*src.channels() + 0)*(*(kernel+kcenter+i));
gmul += *(srcData+y*src.step+(x+i)*src.channels() + 1)*(*(kernel+kcenter+i));
rmul += *(srcData+y*src.step+(x+i)*src.channels() + 2)*(*(kernel+kcenter+i));
}
sum += (*(kernel+kcenter+i));
}
}
if(src.channels() == 1)
{
*(tempData+y*temp.step+x) = mul/sum;
}
else
{
*(tempData+y*temp.step+x*temp.channels()+0) = bmul/sum;
*(tempData+y*temp.step+x*temp.channels()+1) = gmul/sum;
*(tempData+y*temp.step+x*temp.channels()+2) = rmul/sum;
}
}
}
//y方向一维高斯模糊
for(int x = 0; x < temp.cols; x++)
{
for(int y = 0; y < temp.rows; y++)
{
double mul = 0;
sum = 0;
double bmul = 0, gmul = 0, rmul = 0;
for(i = -kcenter; i <= kcenter; i++)
{
if((y+i) >= 0 && (y+i) < temp.rows)
{
if(temp.channels() == 1)
{
mul += *(tempData+(y+i)*temp.step+x)*(*(kernel+kcenter+i));
}
else
{
bmul += *(tempData+(y+i)*temp.step+x*temp.channels() + 0)*(*(kernel+kcenter+i));
gmul += *(tempData+(y+i)*temp.step+x*temp.channels() + 1)*(*(kernel+kcenter+i));
rmul += *(tempData+(y+i)*temp.step+x*temp.channels() + 2)*(*(kernel+kcenter+i));
}
sum += (*(kernel+kcenter+i));
}
}
if(temp.channels() == 1)
{
*(dstData+y*dst.step+x) = mul/sum;
}
else
{
*(dstData+y*dst.step+x*dst.channels()+0) = bmul/sum;
*(dstData+y*dst.step+x*dst.channels()+1) = gmul/sum;
*(dstData+y*dst.step+x*dst.channels()+2) = rmul/sum;
}
}
}
delete[] kernel;
}
该函数中使用的水平方向和垂直方向的高斯矩阵为同一矩阵,实际计算时可根据需要取不同。
模糊效果如图3所示:

比较
使用GetTickCount()进行比较,GetTickCount()函数的精度为1ms。
以下表格中的数据均为作者机器上的某两次运行结果取均值,编程环境为vs2010+opencv2.2

上表中Debug版本的GaussianTemplateSmooth竟然比GaussianSmooth2D运行时间长,难道是二维数组比不上一维指针,或者是Debug版本的问题?实验结果确实如上。
将本文所写函数与opencv2.2提供的高斯模糊函数GaussianBlur一起进行比较。


结论
如上表4,5所示,对GaussianSmooth2D的改进函数GaussianSmooth,当越大时,提速效果越明显,这种速度的改进在Debug模式下尤为明显。无论是在Debug,还是在Release模式下,Opencv2.2提供的GaussianBlur完胜本文所用的函数。建议在学习算法时参考本文内容,实际项目中使用GaussianBlur。
本例代码键连接:http://download.csdn.net/detail/zddmail/4217704
转载请注明出处,如有问题,请联系zddmail@gmail.com.
zdd
2012年4月11日11:53:40