一直对齐次坐标这个概念的理解不够彻底,只见大部分的书中说道“齐次坐标在仿射变换中非常的方便”,然后就没有了后文,今天在一个叫做“三百年
重生”的博客上看到一篇关于透视投影变换的探讨的文章,其中有对齐次坐标有非常精辟的说明,特别是针对这样一句话进行了有力的证明:“齐次坐标表示是计算机图形学的重要手段之一,它既能够用来明确区分向量和点,同时也更易用于进行仿射(线性)几何变换。”——
F.S. Hill, JR。
由于作者对齐次坐标真的解释的不错,我就原封不动的摘抄过来:
对于一个
向量
v
以及基
oabc
,可以找到一组坐标
(v1,v2,v3)
,使得
v
= v1
a
+ v2 b +
v3
c
(
1
)
而对于一个
点
p
,则可以找到一组坐标(
p1,p2,p3
),使得
p
–
o
= p1 a +
p2 b
+ p3 c
(
2
),
从上面对
向量
和
点
的表达,我们可以看出为了在坐标系中表示一个
点
(如
p
),我们把点的位置看作是对这个基的原点
o
所进行的一个位移,即一个向量——
p – o
(有的书中把这样的向量叫做位置向量
——起始于坐标原点的特殊向量),我们在表达这个向量的同时用等价的方式表达出了点
p:p
= o
+ p1 a +
p2 b
+ p3 c (3)
(1)(3)
是坐标系下表达一个
向量
和点
的不同表达方式。这里可以看出,虽然都是用代数分量的形式表达向量和点,但表达一个点比一个向量需要额外的信息。如果我写出一个代数分量表达
(1, 4, 7)
,谁知道它是个向量还是个点!
我们现在把(
1
)(
3
)写成矩阵的形式:v = (v1 v2 v3 0) X (a b c o)
p = (p1 p2 p3 1) X (a b c o),
这里
(a,b,c,o)
是坐标基矩阵,右边的列向量分别是向量
v
和点
p
在基下的坐标。
这样,向量和点在同一个基下就有了不同的表达:3D
向量
的第
4
个代数分量是
0
,而
3D
点
的第
4
个代数分量是
1
。像这种这种用
4
个代数分量表示
3D
几何概念的方式是一种齐次坐标表示。
这样,上面的
(1, 4, 7)
如果写成(
1,4,7,0
),它就是个向量;如果是
(1,4,7,1)
,它就是个点。
下面是如何在普通坐标
(Ordinary Coordinate)
和齐次坐标
(Homogeneous Coordinate)
之间进行转换:
(1)
从普通坐标转换成齐次坐标时
如果
(x,y,z)
是个点,则变为
(x,y,z,1);
如果
(x,y,z)
是个向量,则变为
(x,y,z,0)
(2)从齐次坐标转换成普通坐标时
如果是
(x,y,z,1)
,则知道它是个点,变成
(x,y,z);
如果是
(x,y,z,0)
,则知道它是个向量,仍然变成
(x,y,z)
以上是通过齐次坐标来区分向量和点的方式。从中可以思考得知,对于平移
T
、旋转
R
、缩放
S
这
3
个最常见的仿射变换,平移变换只对于点才有意义,因为普通向量没有位置概念,只有大小和方向.
而旋转和缩放对于向量和点都有意义,你可以用类似上面齐次表示来检测。从中可以看出,齐次坐标用于仿射变换非常方便。
此外,对于一个普通坐标的
点
P=(Px, Py, Pz)
,有对应的一族齐次坐标
(wPx, wPy, wPz, w)
,其中
w
不等于零
。比如,
P(1, 4, 7)
的齐次坐
标有
(1, 4, 7, 1)
、(
2, 8, 14, 2
)、(
-0.1, -0.4, -0.7, -0.1
)等等
。
因此,如果把一个点从普通坐标变成齐次坐标,给
x,y,z
乘上同一个非零数
w
,然后增加第
4
个分量
w
;如果把一个齐
次坐标转换成普通坐标,把
前三个坐标同时除以第
4
个坐标,然后去掉第
4
个分量。
由于齐次坐标使用了
4
个分量来表达
3D
概念,使得平移变换可以使用矩阵进行,从而如
F.S. Hill, JR
所说,仿射(线性)变换的进行
更加方便。由于图形硬件已经普遍地支持齐次坐标与矩阵乘法,因此更加促进了齐次坐标使用,使得它似乎成为图形学中的一个标准。
以上很好的阐释了齐次坐标的作用及运用齐次坐标的好处。其实在图形学的理论中,很多已经被封装的好的API也是很有研究
的,要想成为一名专业的计算机
图形学
的
学习者,除了知其然必须还得知其所以然。
这样在遇到问题的时候才能迅速定位问题的根源,从而解决问题。
另一个帖子的介绍:
http://www.cnblogs.com/kesalin/archive/2009/09/09/homogeneous.html
问题: 两条平行线会相交

铁轨在无限远处相交于一点
在欧几里得几何空间里,两条平行线永远都不会相交。但是在投影空间中,如右图中的两条铁轨在地平线处却是会相交的,因为在无限远处它们看起来相交于一点。
在欧几里得(或称笛卡尔)空间里描述2D/3D 几何物体是很理想的,但在投影空间里面却并不见得。 我们用 (x, y
)
表
示笛卡尔空间中的一个 2D 点,而处于无限远处的点 (∞,∞)
在笛卡尔空间里是没有意义的。投影空间里的两条平行线会在无限远处相交于一点,但笛卡尔空间里面无法搞定这个问题(因为无限远处的点在笛卡尔空间里是没有
意义的),因此数学家想出齐次坐标这个点子来了。
解决办法: 其次坐标
由 August Ferdinand Möbius 提出的齐次坐标(Homogeneous
coordinates)让我们能够在投影空间里进行图像和几何处理,齐次坐标用 N + 1个分量来描述 N 维坐标。比如,2D
齐次坐标是在笛卡尔坐标(X, Y)的基础上增加一个新分量 w,变成(x, y, w),其中笛卡尔坐标系中的大X,Y
与齐次坐标中的小x,y有如下对应关系:
X = x/w
Y = y/w
笛卡尔坐标中的点 (1, 2) 在齐次坐标中就是 (1, 2, 1) 。如果这点移动到无限远(∞,∞)处,在齐次坐标中就是 (1, 2, 0) ,这样我们就避免了用没意义的"∞" 来描述无限远处的点。
为什么叫齐次坐标?
前面提到,我们分别用齐次坐标中的 x 和 y 除以 w 就得到笛卡尔坐标中的 x 和 x,如图所示:

仔细观察下面的转换例子,可以发现些有趣的东西:
上
图中,点 (1, 2, 3), (2, 4, 6) 和 (4, 8, 12) 对应笛卡尔坐标中的同一点 (1/3, 2/3)。
任意数量积的(1a, 2a, 3a) 始终对应于笛卡尔坐标中的同一点 (1/3,
2/3)。因此这些点是“齐次”的,因为他们始终对应于笛卡尔坐标中的同一点。换句话说,齐次坐标描述缩放不变性(scale invariant)。
证明: 两平行线可以相交
笛卡尔坐标系中,对于如下两个直线方程:
![]()
如果 C ≠ D,以上方程组无解;如果 C = D,那这两条线就是同一条线了。
下面我们用 x/w, y/w 代替 x, y 放到投影空间里来求解:
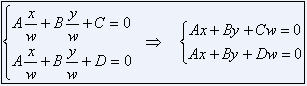
现在我们就可以在 C ≠ D 的情况得到一组解 (x, y, 0),代入得
(C - D)w = 0,因为 C ≠ D,所以 w = 0。因而,两条平行线相交于投影空间中无限远处的一点
(x, y, 0)。
齐次坐标在计算机图形学中是有用的,将 3D 场景投影到 2D 平面的过程中就用到它了。