学步园

前言：在skia中经常会碰到SkFixedToFloat或者相反的操作，将单精度浮点数转成定点数很简单，直接乘个 65536 再强制一 下类型就行了，这也就是 Float2Fixed 所做的。忘了在哪里看到的据说是skia这么做是速度问题。

对于浮点类型的数据采用单精度类型(float)和双精度类型(double)来存储，float数据占用32bit,double数据占用 64bit,我们在声明一个变量float f = 2.25f的时候，是如何分配内存的呢？其实不论是float类型还是double类型，在计算机内存中的存储方式都是遵从IEEE的规范的，float遵从的是IEEE
R32.24 ,而double 遵从的是R64.53。

无论是单精度还是双精度，在内存存储中都分为3个部分： 

1) 符号位(Sign)：0代表正，1代表为负； 

2) 指数位(Exponent)：用于存储科学计数法中的指数数据，并且采用移位存储；

3) 尾数部分(Mantissa)：尾数部分；

其中float的存储方式如下图所示：

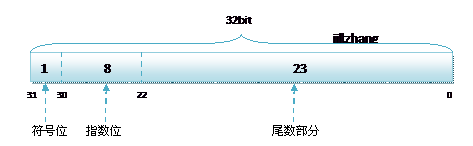
而双精度的存储方式为:

R32.24和R64.53的存储方式都是用科学计数法来存储数据的，比如8.25用十进制的科学计数法表示就为:8.25*,而120.5可以表示为:1.205*。而我们傻蛋计算机根本不认识十进制的数据，它只认识0和1，所以在计算机内存中，首先要将上面的数更改为二进制的科学计数法表示，8.25用二进制表示可表示为1000.01，120.5用二进制表示为：1110110.1。用二进制的科学计数法表示1000.01可以表示为1.00001*，1110110.1可以表示为1.1101101*,任何一个数的科学计数法表示都为1.xxx*,
尾数部分就可以表示为xxxx,第一位都是1嘛，干嘛还要表示呀？可以将小数点前面的1省略，所以23bit的尾数部分，可以表示的精度却变成了24bit，道理就是在这里，那24bit能精确到小数点后几位呢，我们知道9的二进制表示为1001，所以4bit能精确十进制中的1位小数点，24bit就能使float能精确到小数点后6位，而对于指数部分，因为指数可正可负，8位的指数位能表示的指数范围就应该为:-127-128了，
所以指数部分的存储采用移位存储，存储的数据为元数据+127。

下面就看看8.25和120.5在内存中真正的存储方式：

首先看下8.25，用二进制的科学计数法表示为:1.0001*

按照上面的存储方式，符号位为0，表示为正；指数位为3+127=130，位数部分为1.00001，故8.25的存储方式如下：

0xbffff380:    01000001000001000000000000000000

分解如下：0--10000010--00001000000000000000000

符号位为0，指数部分为10000010，位数部分为00001000000000000000000

同理，120.5在内存中的存储格式如下：

0xbffff384:    01000010111100010000000000000000

分解如下：0--10000101--11100010000000000000000

那么如果给出内存中一段数据，并且告诉你是单精度存储的话，你如何知道该数据的十进制数值呢？其实就是对上面的反推过程，比如给出如下内存数据：

01000001001000100000000000000000

第一步：符号位为0，表示是正数；

第二步：指数位为10000010，换算成十进制为130，所以指数为130-127=3；

第三步：尾数位为01000100000000000000000，换算成十进制为(1+1/4+1/64)；

所以相应的十进制数值为：2^3*(1+1/4+1/64)=8+2+1/8=10.125

再看一个例子，观察其输出：

[doyle@phuang algorithm]$ ./a.out 

d1 = 2.2000000476837, d2 = 2.2500000000000

可能输出的结果让大家疑惑不解，单精度的2.2转换为双精度后，精确到小数点后13位后变为了2.2000000476837，而单精度的2.25 转换为双精度后，变为了2.2500000000000，为何2.2在转换后的数值更改了而2.25却没有更改呢？很奇怪吧？其实通过上面关于两种存储结 果的介绍，我们已经大概能找到答案。首先我们看看2.25的单精度存储方式：0
10000000 00100000000000000000000，而2.25的双精度表示为：0 100 0000 0001 0010 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000,这样2.25在进行强制转换的时候，数值是不会变的。我们再看看2.2的单精度和双精度内存表示，2.2用科学计数法表示应该为：将十进制的小数转换为二进制的小数 的方法为将小数*2，取整数部分，所以0.282=0.4，所以二进制小数第一位为0.4的整数部分0，0.4×2=0.8，第二位为
0,0.8*2=1.6,第三位为1，0.6×2 = 1.2，第四位为1，0.2*2=0.4，第五位为0，这样永远也不可能乘到=1.0，得到的二进制是一个无限循环的排列 00110011001100110011... ,对于单精度数据来说，尾数只能表示24bit的精度，所以2.2的float存储为：0 10000000 00011001100110011001101

但是这样存储方式，换算成十进制的值，却不会是2.2的，应为十进制在转换为二进制的时候可能会不准确，如2.2，而double类型的数据也存在同样的问题，所以在浮点数表示中会产生些许的误差，在单精度转换为双精度的时候，也会存在误差的问题，对于能够用二进制表示的十进制数据，如
2.25，这个误差就会不存在，所以会出现上面比较奇怪的输出结果。 

浮点数在内存中的存储表示是以2的负数次方来模拟和逼近的，如果浮点数的小数部分可以用二进制完美地表示，则浮点数转化为二进制存储的时候不会存在精度丢失，否则内存中的这种表示浮点数的方法将会导致浮点数的精度丢失，如上面的2.2；