一个看起来很牛的计算Pi的程序:
int a=10000,b,c=2800,d,e,f[2801],g;
main() {
for(;b-c;)
f[b++]=a/5;
for(;d=0,g=c*2;c -=14,printf("%.4d",e+d/a),e=d%a)
for(b=c; d+=f[b]*a,f[b]=d%--g,d/=g--,--b; d*=b);
}
二、数学公式
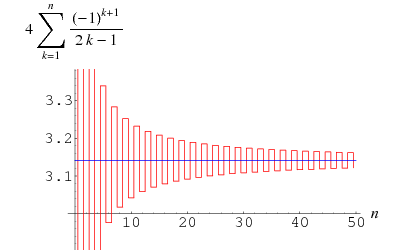
数学家们研究了数不清的方法来计算PI,这个程序所用的公式如下:
1 2 3 k
pi = 2 + --- * (2 + --- * (2 + --- * (2 + ... (2 + ---- * (2 + ... ))...)))
3 5 7 2k+1
就是
Pi/2 = Sum{k!/(2k+1)!!, k=0,1,2,...}
其实上面的程序效率并不高,下面转贴更多Pi的公式,来源于:
http://mathworld.wolfram.com/PiFormulas.html
There are many formulas of ![]() of many types. Among others, these include series, products, geometric constructions, limits, special values, and pi iterations.
of many types. Among others, these include series, products, geometric constructions, limits, special values, and pi iterations.
![]() is intimately related to the properties of circles and spheres. For a circle of radius
is intimately related to the properties of circles and spheres. For a circle of radius ![]() , the circumference and area are given by
, the circumference and area are given by
| (1) | |||
| (2) |
Similarly, for a sphere of radius ![]() , the surface area and volume enclosed are
, the surface area and volume enclosed are
| (3) | |||
| (4) |
An exact formula for ![]() in terms of the inverse tangents of unit fractions is Machin's formula
in terms of the inverse tangents of unit fractions is Machin's formula
| (5) |
There are three other Machin-like formulas, as well as thousands of other similar formulas having more terms.
 |
(6) | ||
| (7) |
(Wells 1986, p. 50), which is known as the Gregory series and may be obtained by plugging ![]() into the Leibniz series for
into the Leibniz series for ![]() . The error after the
. The error after the ![]() th term of this series in the Gregory series is larger than
th term of this series in the Gregory series is larger than ![]() so this sum converges so slowly that 300 terms are not sufficient to calculate
so this sum converges so slowly that 300 terms are not sufficient to calculate ![]() correctly to two decimal places! However, it can be transformed to
correctly to two decimal places! However, it can be transformed to
 |
(8) |
where ![]() is the Riemann zeta function (Vardi 1991, pp. 157-158; Flajolet and Vardi 1996), so that the error after
is the Riemann zeta function (Vardi 1991, pp. 157-158; Flajolet and Vardi 1996), so that the error after ![]() terms is
terms is ![]() .
.
An infinite sum series to Abraham Sharp (ca. 1717) is given by
 |
(9) |
(Smith 1953, p. 311). Additional simple series in which ![]() appears are
appears are
![sum_(k==1)^(infty)[((-1)^(k+1))/(4k+1)+((-1)^(k+1))/(4k-3)]](http://mathworld.wolfram.com/images/equations/PiFormulas/inline35.gif) |
(10) | ||
| (11) | |||
 |
(12) | ||
| (13) | |||
| (14) | |||
| (15) | |||
| (16) | |||
| (17) |
(Wells 1986, p. 53).
In 1666, Newton ![]() used a geometric construction to derive the formula
used a geometric construction to derive the formula
| (18) | |||
| (19) |
which he used to compute ![]() (Wells 1986, p. 50; Borwein et al. 1989; Borwein and Bailey 2003, pp. 105-106). The coefficients can be found from the integral
(Wells 1986, p. 50; Borwein et al. 1989; Borwein and Bailey 2003, pp. 105-106). The coefficients can be found from the integral
| (20) | |||
| (21) |
by taking the series expansion of ![]() about 0, obtaining
about 0, obtaining
| (22) |
(Sloane's A054387 and A054388). Using Euler's ![]() convergence improvement transformation gives
convergence improvement transformation gives
 |
(23) | ||
| (24) | |||
| (25) |
(Beeler et al. 1972, Item 120).
This corresponds to plugging ![]() into the power series for the hypergeometric function
into the power series for the hypergeometric function ![]() ,
,
 |
(26) |
Despite the convergence improvement, series (◇) converges at only one bit/term. At the cost of a square root, Gosper has noted that ![]() gives 2 bits/term,
gives 2 bits/term,
 |
(27) |
and ![]() gives almost 3.39 bits/term,
gives almost 3.39 bits/term,
 |
(28) |
where ![]() is the golden ratio. Gosper also obtained
is the golden ratio. Gosper also obtained
| (29) |
A spigot algorithm for ![]() is given by Rabinowitz and Wagon (1995; Borwein and Bailey 2003, pp. 141-142).
is given by Rabinowitz and Wagon (1995; Borwein and Bailey 2003, pp. 141-142).
More amazingly still, a closed form expression giving a digit-extraction algorithm which produces digits of ![]() (or
(or ![]() ) in base-16 was discovered by Bailey et al. (Bailey et al. 1997, Adamchik and Wagon 1997),
) in base-16 was discovered by Bailey et al. (Bailey et al. 1997, Adamchik and Wagon 1997),
| (30) |
This formula, known as the BBP formula, was discovered using the PSLQ algorithm (Ferguson et al. 1999) and is equivalent to
| (31) |
A similar formula was subsequently discovered by Ferguson, leading to a two-dimensional lattice of such formulas which can be generated by these two formulas given by
 |
(32) |
for any complex value of ![]() (Adamchik and Wagon), giving the BBP formula as the special case
(Adamchik and Wagon), giving the BBP formula as the special case ![]() .
.
There is a series of BPP-type formulas for ![]() in powers of
in powers of ![]() , the first few independent formulas of which are
, the first few independent formulas of which are
 |
(33) | ||
| (34) | |||
| (35) | |||
![sum_(k==0)^(infty)(-1)^k[3/(14k+1)-3/(14k+3)+3/(14k+5)+4/(14k+7)+4/(14k+9)-4/(14k+11)+4/(14k+13)]](http://mathworld.wolfram.com/images/equations/PiFormulas/inline103.gif) |
(36) | ||
![sum_(k==0)^(infty)(-1)^k[2/(18k+1)+3/(18k+3)+2/(18k+5)-2/(18k+7)-2/(18k+11)+2/(18k+13)+3/(18k+15)+2/(18k+17)]](http://mathworld.wolfram.com/images/equations/PiFormulas/inline106.gif) |
(37) | ||
![sum_(k==0)^(infty)(-1)^k[3/(22k+1)-3/(22k+3)+3/(22k+5)-3/(22k+7)+3/(22k+9)+8/(22k+11)+3/(22k+13)-3/(22k+15)+3/(22k+17)-3/(22k+19)+1/(22k+21)].](http://mathworld.wolfram.com/images/equations/PiFormulas/inline109.gif) |
(38) |
Similarly, there are a series of BPP-type formulas for ![]() in powers of
in powers of ![]() , the first few independent formulas of which are
, the first few independent formulas of which are
| (39) | |||
| (40) | |||
![1/(16)sum_(k==0)^(infty)1/(256^k)[(64)/(16k+1)-(32)/(16k+4)-(16)/(16k+5)-(16)/(16k+6)+4/(16k+9)-2/(16k+12)-1/(16k+13)-1/(16k+14)]](http://mathworld.wolfram.com/images/equations/PiFormulas/inline120.gif) |
(41) | ||
![1/(32)sum_(k==0)^(infty)1/(256^k)[(128)/(16k+2)+(64)/(16k+3)+(64)/(16k+4)-(16)/(16k+7)+8/(16k+10)+4/(16k+11)+4/(16k+12)-1/(16k+15)]](http://mathworld.wolfram.com/images/equations/PiFormulas/inline123.gif) |
(42) | ||
![1/(32)sum_(k==0)^(infty)1/(4096^k)[(256)/(24k+2)+(192)/(24k+3)-(256)/(24k+4)-(96)/(24k+6)-(96)/(24k+8)+(16)/(24k+10)-4/(24k+12)-3/(24k+15)-6/(24k+16)-2/(24k+18)-1/(24k+20)]](http://mathworld.wolfram.com/images/equations/PiFormulas/inline126.gif) |
(43) | ||
![1/(64)sum_(k==0)^(infty)1/(4096^k)[(256)/(24k+1)+(256)/(24k+2)-(384)/(24k+3)-(256)/(24k+4)-(64)/(24k+5)+(96)/(24k+8)+(64)/(24k+9)+(16)/(24k+10)+8/(24k+12)-4/(24k+13)+6/(24k+15)+6/(24k+16)+1/(24k+17)+1/(24k+18)-1/(24k+20)-1/(24k+21)]](http://mathworld.wolfram.com/images/equations/PiFormulas/inline129.gif) |
(44) | ||
![1/(96)sum_(k==0)^(infty)1/(4096^k)[(256)/(24k+2)+(64)/(24k+3)+(128)/(24k+5)+(352)/(24k+6)+(64)/(24k+7)+(288)/(24k+8)+(128)/(24k+9)+(80)/(24k+10)+(20)/(24k+12)-(16)/(24k+14)-1/(24k+15)+6/(24k+16)-2/(24k+17)-1/(24k+19)+1/(24k+20)-2/(24k+21)]](http://mathworld.wolfram.com/images/equations/PiFormulas/inline132.gif) |
(45) | ||
![1/(96)sum_(k==0)^(infty)1/(4096^k)[(256)/(24k+1)+(320)/(24k+3)+(256)/(24k+4)-(192)/(24k+5)-(224)/(24k+6)-(64)/(24k+7)-(192)/(24k+8)-(64)/(24k+9)-(64)/(24k+10)-(28)/(24k+12)-4/(24k+13)-5/(24k+15)+3/(24k+17)+1/(24k+18)+1/(24k+19)+1/(24k+21)-1/(24k+22)]](http://mathworld.wolfram.com/images/equations/PiFormulas/inline135.gif) |
(46) | ||
![1/(96)sum_(k==0)^(infty)1/(4096^k)[(512)/(24k+1)-(256)/(24k+2)+(64)/(24k+3)-(512)/(24k+4)-(32)/(24k+6)+(64)/(24k+7)+(96)/(24k+8)+(64)/(24k+9)+(48)/(24k+10)-(12)/(24k+12)-8/(24k+13)-(16)/(24k+14)-1/(24k+15)-6/(24k+16)-2/(24k+18)-1/(24k+19)-1/(24k+20)-1/(24k+21)]](http://mathworld.wolfram.com/images/equations/PiFormulas/inline138.gif) |
(47) | ||
![1/(4096)sum_(k==0)^(infty)1/(65536^k)[(16384)/(32k+1)-(8192)/(32k+4)-(4096)/(32k+5)-(4096)/(32k+6)+(1024)/(32k+9)-(512)/(32k+12)-(256)/(32k+13)-(256)/(32k+14)+(64)/(32k+17)-(32)/(32k+20)-(16)/(32k+21)-(16)/(32k+22)+4/(32k+25)-2/(32k+28)-1/(32k+29)-1/(32k+30)]](http://mathworld.wolfram.com/images/equations/PiFormulas/inline141.gif) |
(48) | ||
![1/(4096)sum_(k==0)^(infty)1/(65536^k)[(32768)/(32k+2)+(16384)/(32k+3)+(16384)/(32k+4)-(4096)/(32k+7)+(2048)/(32k+10)+(1024)/(32k+11)+(1024)/(32k+12)-(256)/(32k+15)+(128)/(32k+18)+(64)/(32k+19)+(64)/(32k+20)-(16)/(32k+23)+8/(32k+26)+4/(32k+27)+4/(32k+28)-1/(32k+31)].](http://mathworld.wolfram.com/images/equations/PiFormulas/inline144.gif) |
(49) |
F. Bellard found the rapidly converging BBP-type formula
 |
(50) |
A related integral is
| (51) |
(Dalzell 1944; Dalzell 1971; Le Lionnais 1983, p. 22; Borwein et al. 2004, p. 3; Boros and Moll 2004, p. 125; Lucas 2005; Borwein et al. 2006, p. 14). This integral was known by K. Mahler in the mid-1960s and appears in an exam at the University of Sydney in November 1960 (Borwein et al. 2004, p. 3). Beukers (2000) and Boros and Moll (2004, p. 126) state this it is not clear if these exists a natural choice of rational polynomial whose integral between 0 and 1 produces ![]() , where 333/106 is the next convergent. However, an integral exists for the fourth convergent, namely
, where 333/106 is the next convergent. However, an integral exists for the fourth convergent, namely
| (52) |
(Lucas 2005; Bailey et al. 2006, p. 219). In fact, Lucas (2005) gives a few other such integrals.
Backhouse (1995) used the identity
| (53) | |||
 |
(54) | ||
| (55) |
for positive integer ![]() and
and ![]() and where
and where ![]() ,
, ![]() , and
, and ![]() are rational constant to generate a number of formulas for
are rational constant to generate a number of formulas for ![]() . In particular, if
. In particular, if ![]() , then
, then ![]() (Lucas 2005).
(Lucas 2005).
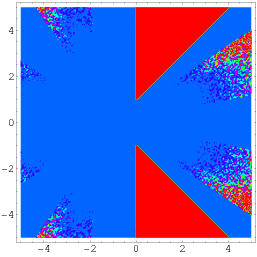
An even more general identity due to Wagon is given by
![pi+4tan^(-1)z+2ln((1-2z-z^2)/(z^2+1))
==sum_(k==0)^infty1/(16^k)[(4(z+1)^(8k+1))/(8k+1)-(2(z+1)^(8k+4))/(8k+4)-((z+1)^(8k+5))/(8k+5)-((z+1)^(8k+6))/(8k+6)]](http://mathworld.wolfram.com/images/equations/PiFormulas/equation15.gif) |
(56) |
(Borwein and Bailey 2003, p. 141), which holds over a region of the complex plane excluding two triangular portions symmetrically placed about the real axis, as illustrated above.
Following the discovery of the base-16 digit BBP formula and related formulas, similar formulas in other bases were investigated. Borwein and Galway have recently shown that there is no non-binary Bailey-Borwein-Plouffe-type formula, although this does not rule out a completely different scheme for digit extraction algorithms in other bases (Bailey 2002).
S. Plouffe has devised an algorithm to compute the ![]() th digit of
th digit of ![]() in any base in
in any base in ![]() steps.
steps.
A slew of additional identities due to Ramanujan ![]() , Catalan, and Newton
, Catalan, and Newton ![]() are given by Castellanos (1988, pp. 86-88), including several involving sums of Fibonacci numbers. Ramanujan found
are given by Castellanos (1988, pp. 86-88), including several involving sums of Fibonacci numbers. Ramanujan found
![sum_(k==0)^infty((-1)^k(4k+1)[(2k-1)!!]^3)/([(2k)!!]^3)==sum_(k==0)^infty((-1)^k(4k+1)[Gamma(k+1/2)]^3)/(pi^(3/2)[Gamma(k+1)]^3)==2/pi](http://mathworld.wolfram.com/images/equations/PiFormulas/equation16.gif) |
(57) |
(Hardy 1923; Hardy 1924; Hardy 1999, p. 7).
Plouffe (2006) found the beautiful formula
| (58) |
An interesting infinite product formula due to Euler which relates ![]() and the
and the ![]() th prime
th prime ![]() is
is
![2/(product_(n==1)^(infty)[1+(sin(1/2pip_n))/(p_n)])](http://mathworld.wolfram.com/images/equations/PiFormulas/inline171.gif) |
(59) | ||
![2/(product_(n==2)^(infty)[1+((-1)^((p_n-1)/2))/(p_n)])](http://mathworld.wolfram.com/images/equations/PiFormulas/inline174.gif) |
(60) |
(Blatner 1997, p. 119), plotted above as a function of the number of terms in the product.
A method similar to Archimedes' ![]() can be used to estimate
can be used to estimate ![]() by starting with an
by starting with an ![]() -gon and then relating the area of subsequent
-gon and then relating the area of subsequent ![]() -gons. Let
-gons. Let ![]() be the angle from the center of one of the polygon's segments,
be the angle from the center of one of the polygon's segments,
| (61) |
then
| (62) |
(Beckmann 1989, pp. 92-94).
Vieta (1593) was the first to give an exact expression for ![]() by taking
by taking ![]() in the above expression, giving
in the above expression, giving
| (63) |
which leads to an infinite product of nested radicals,
 |
(64) |
(Wells 1986, p. 50; Beckmann 1989, p. 95). However, this expression was not rigorously proved to converge until Rudio (1892).
A related formula is given by
 |
(65) |
which can be written
| (66) |
where ![]() is defined using the iteration
is defined using the iteration
![pi_n==sqrt((1/2pi_(n-1))^2+[1-sqrt(1-(1/2pi_(n-1))^2)]^2)](http://mathworld.wolfram.com/images/equations/PiFormulas/equation24.gif) |
(67) |
with ![]() (J. Munkhammar, pers. comm., April 27, 2000). The formula
(J. Munkhammar, pers. comm., April 27, 2000). The formula
![pi==2lim_(m->infty)sum_(n==1)^msqrt([sqrt(1-((n-1)/m)^2)-sqrt(1-(n/m)^2)]^2+1/(m^2))](http://mathworld.wolfram.com/images/equations/PiFormulas/equation25.gif) |
(68) |
is also closely related.
A pretty formula for ![]() is given by
is given by
 |
(69) |
where the numerator is a form of the Wallis formula for ![]() and the denominator is a telescoping sum with sum 1/2 since
and the denominator is a telescoping sum with sum 1/2 since
| (70) |
(Sondow 1997).
A particular case of the Wallis formula gives
![pi/2==product_(n==1)^infty[((2n)^2)/((2n-1)(2n+1))]==(2.2)/(1.3)(4.4)/(3.5)(6.6)/(5.7)...](http://mathworld.wolfram.com/images/equations/PiFormulas/equation28.gif) |
(71) |
(Wells 1986, p. 50). This formula can also be written
![lim_(n->infty)(2^(4n))/(n(2n; n)^2)==pilim_(n->infty)(n[Gamma(n)]^2)/([Gamma(1/2+n)]^2)==pi,](http://mathworld.wolfram.com/images/equations/PiFormulas/equation29.gif) |
(72) |
where ![]() denotes a binomial coefficient and
denotes a binomial coefficient and ![]() is the gamma function (Knopp 1990). Euler
is the gamma function (Knopp 1990). Euler ![]() obtained
obtained
| (73) |
which follows from the special value of the Riemann zeta function ![]() . Similar formulas follow from
. Similar formulas follow from ![]() for all positive integers
for all positive integers ![]() .
.
An infinite sum due to Ramanujan ![]() is
is
 |
(74) |
(Borwein et al. 1989; Borwein and Bailey 2003, p. 109; Bailey et al. 2006, p. 44). Further sums are given in Ramanujan ![]() (1913-14),
(1913-14),
| (75) |
and
|
|