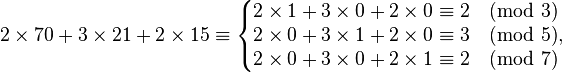现在的位置: 首页 > 综合 > 正文

中国剩余定理 算法摘记

2017年11月22日 ⁄ 综合 ⁄ 共 540字 ⁄ 字号 小 中 大 ⁄ 评论关闭

中国剩余定理是数论中的一个关于一元线性同余方程组的定理，说明了一元线性同余方程组有解的准则以及求解方法。也称为孙子定理。


用现代数学的语言来说明的话，中国剩余定理给出了以下的一元线性同余方程组：


中国剩余定理说明：假设整数m1, m2,
... , mn两两互质，则对任意的整数：a1, a2,
... , an，方程组(S)有解，并且通解可以用如下方式构造得到：

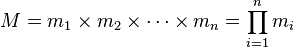  1. 设M = m_1 \times m_2 \times \cdots \times m_n = \prod_{i=1}^n m_i是整数m1, m2,
    ... , mn    的乘积，并设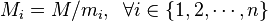M_i = M/m_i, \; \; \forall i \in \{1, 2, \cdots , n\}是除了mi以外的n -
    1    个整数的乘积。
  2. 设t_i = M_i^{-1}为M_i模m_i的数论倒数：t_i M_i \equiv 1 \pmod {m_i}, \; \; \forall i \in \{1, 2, \cdots , n\}.
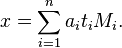
  3. 方程组(S)的通解形式为：x = a_1 t_1 M_1 + a_2 t_2 M_2 + \cdots + a_n t_n M_n + k M= k M + \sum_{i=1}^n a_i t_i M_i, \quad k \in \mathbb{Z}. 在模M的意义下，方程组(S)只有一个解：x = \sum_{i=1}^n a_i t_i M_i.

例子

使用中国剩余定理来求解上面的“物不知数”问题，便可以理解《孙子歌诀》中的数字含义。这里的线性同余方程组是：

(S) : \quad \left\{ \begin{matrix} x \equiv 2 \pmod {3} \\ x \equiv 3 \pmod {5} \\ x \equiv 2 \pmod {7} \end{matrix} \right.

三个模数m1=3, m2=5, m3=7的乘积是M=105，对应的M1=35, M2=21, M3=15. 

 35%3 21%5 15%7

而可以计算出相应的数论倒数：t1=2, t2=1, t3=1. 

所以《孙子歌诀》中的70，21和15其实是这个“物不知数”问题的基础解：

70 = 2 \times 35 \equiv \left\{ \begin{matrix} 1 \pmod {3} \\ 0 \pmod {5} \\ 0 \pmod {7} \end{matrix} , \right. 21 = 1 \times 21 \equiv \left\{ \begin{matrix} 0 \pmod {3} \\ 1 \pmod {5} \\ 0 \pmod {7} \end{matrix} , \right. 15 = 1 \times 15 \equiv \left\{ \begin{matrix} 0 \pmod {3} \\ 0 \pmod {5} \\ 1 \pmod {7} \end{matrix} , \right.

而将原方程组中的余数相应地乘到这三个基础解上，再加起来，其和就是原方程组的解：

2\times 70 + 3 \times 21 + 2 \times 15 \equiv \left\{ \begin{matrix} 2 \times 1 + 3 \times 0 + 2 \times 0 \equiv 2 \pmod {3} \\ 2 \times 0 + 3 \times 1 + 2 \times 0 \equiv 3 \pmod {5} \\ 2 \times 0 + 3 \times 0 + 2 \times 1 \equiv 2 \pmod {7} \end{matrix} , \right.

这个和是233，实际上原方程组的通解公式为：

x = 233 + k \times 105, \; k\in \mathbb{Z}.

《孙子算经》中实际上给出了最小正整数解，也就是k=-2时的解：x=23.

不互质版本的

HDU 3579



返回
【上篇】
【下篇】

作者:

抱歉!评论已关闭.

返回首页

Copyright © 2013-2018 学步园  保留所有权利.
软文销售 QQ客服：2265327166 点击这里给我发消息（其他合作也可洽谈）
必威体育
必威电竞