本章主要讨论的是勾股数组,也就是关于满足a^2+b^2=c^2的三元组(a,b,c)的问题。
其实,对于勾股数组的个数进行讨论并没有多大意义,因为已知a,b,c为勾股数组,那么显然有da,db,dc(d>0)也为勾股数组,因为(da)^2+(db)^2=d^2(a^+b^2)=d^2c^2=(dc)^2。
因此着重研究的是关于本原勾股数组的问题,本原勾股数组即为a,b,c为勾股数组且满足a,b,c的最大公约数为1。
对于本原勾股数组,显然a和b奇偶性不同只需要将a=2x+1,b=2y+1,c=2z代入a^2+b^2=c^2即可推出有公约数2。由于a和b奇偶性不同,那么显然c为奇数。
那么最关心的是如何求出所有的本原勾股数组。
如果将公式转化一下,得到a^2=c^2-b^2=(c+b)(c-b),那么显然有,c+b和c-b没有公因子,用反证法证明:
如果d|(c+b)且d|(c-b),那么显然有d|((c+b)+(c-b))和d|((c+b)-(c-b))即d|2b且d|2c,因为在定义本原勾股数组的时候已经有了b和c的最大公约数是1的约定(虽然定义是a,b,c最大公约数是1,但是如果gcd(b,c)=d>1,显然有d|c不满足定义)。所以d要么为1,要么为2。但是如果d=2时,那么显然a,b,c均为偶数,不满足定义,那么d只能为1,证明了c+b和c-b没有公因子。
因此,如果将a^2进行质因数分解,那么会有a=p1^t1*p2^t2*p3^t3...pn^tn,其中指数t1,t2,t3...tn为偶数(因为这样才能保证a^2开根号后为整数),又因为c+b和c-b没有公因数,所以c+b和c-b各取a分解后的其中某一些pk^tk,因此,c+b和c-b均为平方数。那么假设c+b=s^2,c-b=t^2,则有c=(s^2+t^2)/2,b=(s^2-t^2)/2,a=st,因此形如(st,(s^2-t^2)/2,(s^2+t^2)/2)的三元组为本原勾股数组。(其中s和t都是奇数,因为如果s和t中有且只有一个为奇数,那么显然(s^2+t^2)/2不会是整数,而如果两个数都是偶数,那么显然该三元组有公因子2,与本原勾股数组定义矛盾。)
接下来谈谈勾股定理的证明(书上第二章并没有对勾股定理的证明进行讨论)
在书《proofs without words》
中有如下几种证明方法证明勾股定理
中有如下几种证明方法证明勾股定理
直接上图:
1.这个是周髀算经里的证明方法

2.古印度数学家婆什迦罗也给出了一种证明方法
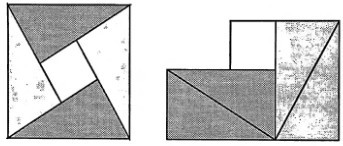
3.根据欧几里得的证明方法可得到如下证法
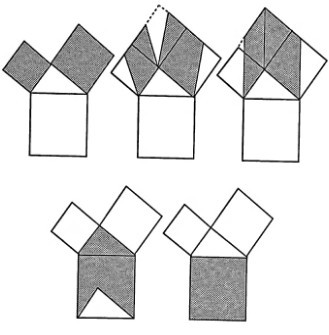
4.英国思维游戏之父也给出了一种证明方法
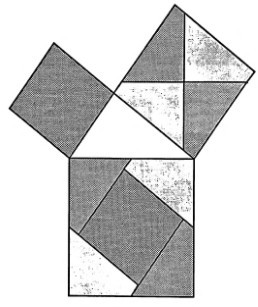
5.有趣的是,书里还收录了美国第20任总统加菲尔德的一种证明方法

虽然用图形有时候并不能一眼给出十分严谨的代数证明,但是,它具有很强的直观性。据说在Loomis的《Pythagoras Proposition》中,给出了367种勾股定理的证明方式,但是很可惜,我在网上貌似没有找到这本书,但是,在这里
给出了近100种证明方法。
给出了近100种证明方法。
习题2.1
(a)关于a或b必是3的倍数的证明。
照例用反证法。
假设a和b都不是3的倍数,那么由于a和b的奇偶性不同,因此我想的方法是分成4种情况讨论
首先由于a和b具有互换性,因此假定a为奇数,b为偶数。
情况1:a mod 3=1,b mod 3=1
那么a=6x+1,b=6y+4,c=6z+5,代入a^2+b^2=c^2后可得
36x^2+12x+1+36y^2+48y+16=36z^2+60z+25
整理后可得3(12x^2+4x+12y^2+16y-12z^2-20z)=8,3不是8的因子,所以显然找不到整数x,y使得该式成立。
情况2:a mod 3=1,b mod 3=2
那么有a=6x+1,b=6y+2,c=6y+5,代入后可得
36x^2+12x+1+26y^2+24y+4=26y^2+60z+25
整理后常数项20也不是3的因子,所以找不到整数x,y
同理,可证明情况3:a mod 3=2,b mod 3=1和情况4:a mod 3=2,b mod 3=2中找不到x,y成立,因此假设不成立,所以证明了a或者b必定是3的倍数。
另外,可以发现,只要a和b不是3的倍数,那么显然会存在c^2 mod 3=2,这是因为1^2 mod 3=2^2 mod 3=1,因此,不管a和b模3得到的数是1还是2,c^2模3后一定是2。那么,对于形如3k+2的数显然不是平方数。(因为x^2=(x mod 3)^2 (mod 3))那么根据1^2 mod 3=2^2 mod 3=1,得到不存在平方数形如3k+2,因此可以得出如果a和b都不是3的倍数,那么c^2不是平方数,问题得证。
(b)关于a或b或c是5的倍数的猜测及证明
观察了很多组本原勾股数组,猜测得a或b或c是5的倍数。
用上一题的枚举加反证法,也可以证明出这个结论,但是上题有个不用枚举就能得出结果的方法,这题有么?
用上一题的第二种方法,可以得出t^2 mod 5=1或4,用1或4组合相加,可以得出c^2 mod 5=2或4或0,就拿0来说,存在c^2 mod 5=0的平方数,所以上题的第二种方法在这里行不通。是否有更简便的方法?求指点。
习题2.2
若d|m和d|n,则d|(m-n)且d|(m+n)的证明。
很显然有m=ad,n=bd,则m-n=d(a-b),m+n=d(a+b),显然能够被d整除。
习题2.3
关于哪些数可以出现在本原勾股数组中的问题。
打表大概的猜想是这样的,除了1以外的奇数都可以出现在本原勾股数组中,偶数除了形如4n+2以外也都能出现在本原勾股数组中,这是不完全归纳,因为不排除a很小,b、c很大的情况就不在我打表的范围之内,我设置a=200,b=c=5000的结果,观察前100个数是这样的。
先研究奇数情况,打表观察奇数在a,b,c三个位置出现的情况(在这里假定a<b),可以惊奇的发现,位置a可以为100以内所有除了1以外的奇数,而且当a=2k+1时总能组成b和c相差1的本原勾股数组(a,b,c)。我们假设a=2k+1,那么会有b=2k(k+1),c=2k(k+1)+1。也就证明了除了1外的奇数都可以出现在本原勾股数组(a,b,c)中,而且,都可以出现在a中。
先研究奇数情况,打表观察奇数在a,b,c三个位置出现的情况(在这里假定a<b),可以惊奇的发现,位置a可以为100以内所有除了1以外的奇数,而且当a=2k+1时总能组成b和c相差1的本原勾股数组(a,b,c)。我们假设a=2k+1,那么会有b=2k(k+1),c=2k(k+1)+1。也就证明了除了1外的奇数都可以出现在本原勾股数组(a,b,c)中,而且,都可以出现在a中。
考虑偶数的情况,上面说了,据不完全归纳,4n+2以外的数都可以出现在本原勾股数组中,先看a形如4n的情况,通过打表可以看出貌似当a=4n的时候都有b和c相差2的情况。假设a=4k,则会出现b=4k^2-1,c=4k^2+1的情况。也就说明了4的倍数都会出现在本原勾股数组中。试着证明下形如4n+2的数不会出现在本原勾股数组中。由于给出了勾股数组的表示形式(st,(s^2-t^2)/2,(s^2+t^2)/2),因此可以得出st为奇数,即4n+2=(s^2-t^2)/2,变形后可得(s+t)(s-t)=4(2n+1),考虑如果s+t和s-t一奇一偶,那么显然s和t不是整数,那么由于有系数4,所以s+t和s-t只可能是两个偶数,也就是说s+t=2(2n+1),s-t=2,可以得出s=2n+2,与定义中s为奇数矛盾,因此4n+2不可能出现在本原勾股数组中。
综上所述,奇数和4的倍数可出现在本原勾股数组中,而形如4n+2的偶数不可能出现在本原勾股数组中。
习题2.4
关于相同c值的本原勾股数组。
通过打表是可以找出相同c值的两个本原勾股数组,也可以找出有相同c值的4个,但是找不到三个,是没有三个的还是存在但是c太大没有找到?在此求解。还有个问题,如何把具有相同c值的多个本原勾股数组的所有c值求到,打表后并没有发现什么明显的规律,但是显然需要满足存在多组奇数<p1,p2>满足p1^2+p2^2的值相同。但是具有这种特征的p1^2+p2^2的值是否有满足规律?求解。
习题2.5
关于三角数和本原勾股数组间的关系
b=4T1:(3,4,5)
b=4T2:(5,12,13)
b=4T3:(7,24,25)
b=4T4:(9,40,41)
估计可以看出规律:第一个数是奇数,第二个数是Tn,第三个数是(Tn)+1,回到习题2.3我们推出的结论:a=2k+1,b=2k(k+1),c=2k(k+1)+1,显然可以看出b是三角数的4倍,那么该规律成立。
习题2.6
关于b+2=c的问题
同样回到习题2.3中,我们推出的结论:a=4k,b=4k^2-1,c=4k^2+1,即为b+2=c的通项公式。
习题2.7
关于2c-2a的规律问题
打表发现2c-2a为完全平方数
试着进行证明:2c-2a=((s^2+t^2)/2-st)*2=(s-t)^2。证毕。