格 (数学)
在数学中,格是其非空有限子集都有一个上确界(叫并)和一个下确界(叫交)的偏序集合(poset)。格也可以特征化为满足特定公理恒等式的代数结构。因为两个定义是等价的,格理论从序理论和泛代数二者提取内容。半格包括了格,依次包括海廷代数和布尔代数。这些"格样式"的结构都允许序理论和抽象代数的描述。
目录[隐藏] |
[编辑]序理论定义
考虑偏序集合(L,≤)。L 是一个格,如果
x 与 y 的并和交分别被指示为  和
和 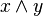 。因为假定并和交存在于格中,
。因为假定并和交存在于格中,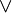 和
和 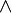 是二元运算。所以这个定义等价于要求 L 是并半格和交半格二者。
是二元运算。所以这个定义等价于要求 L 是并半格和交半格二者。
有界格有一个最大元素和一个最小元素,按惯例分别指示为
1 和 0(也叫做顶和底)。任何格都可以通过增加一个最大元素和最小元素而转换成有界格。
使用容易的归纳论证,你可以演绎出任何格的所有非空有限子集的上确界(并)和下确界(交)的存在。一个很重要的格的种类是完全格。一个格是完全的,如果它的所有子集都有一个交和一个并,这对比于上述格的定义,这里只要求所有非空有限子集的交和并的存在。
[编辑]抽象代数定义
另一种定义格的方式是将格定义为一种代数结构。一个格是一个代数结构 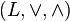 ,其中
,其中 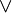 和
和 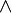 是定义在集合
是定义在集合  上的二元运算,且对于所有的
上的二元运算,且对于所有的 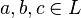 满足:
满足:
从上述三个公理恒等式可以得出重要的:
-
幂等律: 
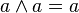
这些公理断言了 (L,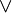 )
)
和 (L,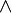 )
)
都是半格。吸收律是唯一交和并都出现了的公理,把格同一对半格区别开来并确保这两个半格正确的交互。特别是,每个半格都是另一个半格的对偶。“有界格”要求交和并都有一个零(neutral)元素,分别习惯叫做
1 和 0。参见半格条目。
格与广群家族有一些联系。因为交和并都符合交换律和结合律。格可以看作由有相同的承载者的两个交换半群组成的。如果格是有界的,这些半群也是交换幺半群。吸收律是特定于格理论的唯一定义恒等式。
L 闭包于交和并之下,通过归纳,蕴涵了 L 的任何有限子集的交和并的存在性,有着一个例外:空集的交和并分别是最大元素和最小元素。所以格只在它是有界的条件下包含所有有限(包含空)交和并。为此有些作者定义格的时候要求
0 和 1 是 L 的成员。而以这种方式定义格不损失一般性,因为任何格都可以被嵌入一个有界格中,这里不接受这种定义。
格的代数解释在泛代数中扮演根本性角色。
[编辑]两个定义的等价性
格的代数定义蕴涵了序理论的定义,反之亦然。
明显的,序理论的格引发了两个二元运算 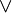 和
和 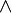 。容易看出这些运算使
。容易看出这些运算使
(L, 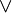 ,
, 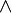 )
)
变成代数意义上的格。反之亦真:考虑代数定义的格 (M, 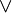 ,
, 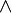 )。现在定义在M 上的偏序
)。现在定义在M 上的偏序
≤ 如下,对于 M 中的元素 x 和 y
-
x ≤ y 当且仅当 x = x
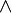 y
y
或等价的
-
x ≤ y 当且仅当 y = x
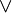 y
y
吸收律确保了两个定义实际上是等价的。你现在可以检查以这种方式介入的关系 ≤ 定义了在其中二元交和并是通过最初运算 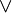 和
和 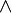 而给出的一个偏序。反过来,由得出自上述序理论公式的代数定义的格
而给出的一个偏序。反过来,由得出自上述序理论公式的代数定义的格
(L, 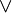 ,
, 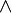 )
)
引发的次序一致于 L 的最初次序。
因为格的两个定义是等价的,你可以随意调用任何定义的适合你用的方面。
[编辑]例子
- 对于任何集合 A,A 的所有子集的搜集(叫做 A 的幂集)可以通过子集包含的次序获得一个以 A 自身和空集为上下界的格。集合的交集和并集分别解释为交(meet)和并(join)。
- 对于任何集合 A,A 的所有有限子集的搜集,通过包含次序也是格,并且将是有界的当且仅当 A 是有限的。
- 自然数(包括 0)在“极小值”(min)和“极大值”(max)运算下,按照通常次序形成格。0 是底,没有顶。
- 自然数的笛卡尔平方,按有随后定义的 ≤ 排序是格,(a,b)
≤ (c,d) ↔ (a ≤ c) & (b ≤ d)。(0,0) 是底;没有顶。 - 正整数在采用最大公约数和最小公倍数运算之下,用整除作为次序关系也形成一个格: a ≤ b 如果 a 整除 b。底是
1;没有顶。 - 任何完全格都是(非常特殊的)有界格。这个类别引出了大量实际例子。
[编辑]格的态射
在两个格之间的适当的态射概念可以轻易的同上述代数定义得出。给定两个格 (L, 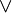 ,
, 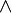 )
)
和 (M,  ,
, 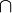 ),格的同态是一个函数 f : L → M 使得
),格的同态是一个函数 f : L → M 使得
-
f(x
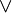 y)
y)
= f(x) f(y),
f(y), -
f(x
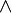 y)
y)
= f(x)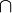 f(y)。
f(y)。
所以 f 是两个底层半格的同态。当考虑带有更多结构的格的时候,这个态射也应当注意这个额外结构。所以在两个有界格 L 和 M 之间的态射 f 还有下列性质:
- f(0L) = 0M ,
- f(1L) = 1M 。
在序理论公式中,这些条件只声称格的同态是保持二元交和并的一个函数。对于有界格,最小和最大元素的保持只是空集的并和交的保持。
格的任何同态必然关于相关的次序关系是单调的;参见极限的保持。反过来当然不是真的:单调性决不蕴涵要求的保持性质。
假定同构作为可逆态射的标准定义,格的同构就是双射格同态。格和它们的态射形成了一个范畴。
[编辑]子格
格 L 的子格是 L 的非空子集,它是带有同 L 一样的交和并运算的格。就是说,如果 L 是一个格,而 M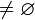 是 L 的子集使得对于 M 中的所有元素对 a, b 有 a
是 L 的子集使得对于 M 中的所有元素对 a, b 有 a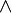 b和 a
b和 a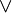 b 在 M 中,则 M 是 L 的子格。[1]
b 在 M 中,则 M 是 L 的子格。[1]
格 L 的子格 M 是 L 的凸子格,如果 x ≤ z ≤ y 和 x, y 在 M 中蕴涵了 z 属于 M,对于在 L 中的所有元素 x, y, z。
[编辑]对偶原理
设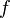 是含有格中的元素以及符号
是含有格中的元素以及符号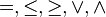 的逻辑命题,令
的逻辑命题,令 是将
是将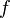 中的
中的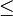 替换为
替换为 ,将
,将 替换为
替换为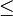 ,将
,将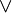 替换为
替换为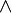 ,将
,将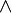 替换为
替换为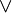 后所得到的命题。则称
后所得到的命题。则称 是
是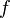 的对偶命题。
的对偶命题。
设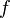 是含有格中的元素以及符号
是含有格中的元素以及符号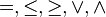 的逻辑命题,若
的逻辑命题,若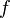 对于一切格为真,则
对于一切格为真,则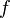 的对偶命题
的对偶命题 也对于一切格为真。
也对于一切格为真。
[编辑]引用
可在线免费获得的专著:
- Burris, Stanley N., and H.P. Sankappanavar, H. P., 1981. A
Course in Universal Algebra. Springer-Verlag. ISBN
3-540-90578-2.
- Jipsen, Peter, and Henry Rose, Varieties
of Lattices, Lecture Notes in Mathematics 1533, Springer Verlag, 1992. ISBN
0-387-56314-8.
Elementary texts recommended for those with limited mathematical maturity:
- Donnellan, Thomas, 1968. Lattice Theory. Pergamon.
- Grätzer, G., 1971. Lattice Theory: First concepts and distributive lattices. W. H. Freeman.
The standard contemporary introductory text:
- Davey, B.A., and H. A. Priestley, 2002. Introduction to Lattices and Order. Cambridge University Press.
The classic advanced monograph:
- Garrett Birkhoff,1967. Lattice
Theory, 3rd ed. Vol. 25 of American Mathematical Society Colloquium Publications. American Mathematical Society.
Free lattices are discussed in the following title, not primarily devoted to lattice theory:
- Johnstone, P.T., 1982. Stone spaces. Cambridge Studies in Advanced Mathematics 3. Cambridge University Press.
The standard textbook on free lattices:
- R. Freese, J. Jezek, and J. B. Nation, 1985. "Free Lattices". Mathematical Surveys and Monographs Volume: 42, American Mathematical Association.
[编辑]注解
- ^ Burris,
Stanley N., and H.P. Sankappanavar, H. P., 1981. A Course
in Universal Algebra. Springer-Verlag. ISBN
3-540-90578-2.






