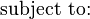Slater's condition
|
|
This article may be confusing or unclear to readers. Please help clarify the article; suggestions may be found on the talk page. (October 2011) |
|
|
This article may be too technical for most readers to understand. Please help improve this article to make it understandable to non-experts, without removing the technical details. The talk page may contain suggestions. (October 2011) |
In mathematics, Slater's condition (or Slater
condition) is a sufficient condition for strong
duality to hold for a convex optimization problem. This is a specific example of a constraint
qualification. In particular, if Slater's condition holds for the primal problem,
then the duality gap is 0, and if the dual value is finite then it is attained.[1]
[edit]Mathematics
Given the problem
with 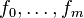 convex (and
convex (and
therefore a convex optimization problem). Then strong duality holds if there exists an 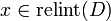 (where
(where
relint is the relative interior and 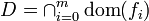 )
)
such that
-
 and
and -
 [2]
[2]
If the first 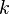 constraints,
constraints,  are linear
are linear
functions, then strong duality holds if there exists an 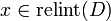 such
such
that
-

-
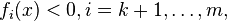 and
and -
 [2]
[2]
[edit]Generalized
Inequalities
Given the problem
where  is
is
convex and  is
is  -convex
-convex
for each 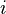 .
.
Then Slater's condition says that if there exists an 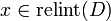 such
such
that
-
 and
and -
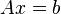
then strong duality holds.[2]
[edit]References
- ^ Borwein,
Jonathan; Lewis, Adrian (2006). Convex Analysis and Nonlinear Optimization: Theory and Examples (2 ed.). Springer. ISBN 978-0-387-29570-1. - ^ a b c Boyd,
Stephen; Vandenberghe, Lieven (2004) (pdf). Convex Optimization.
Cambridge University Press. ISBN 978-0-521-83378-3.
Retrieved October 3, 2011.